Differentiation of function , when different function are in product form Product Rule
You are browsing archives for
Category: Differenciation
Differentiation(Power Rule)
Differentiation is process of finding rates of change of one quantity compared to another. We need differentiation when the rate of change is not constant. Also it is process of finding derivative from function. As well as gradient of tangent to the curve. Differentiation (Power Rule)
Maxima and minima
A high point of curve is called a maxima. A low point is called a minima. In the Curve only one global maxima or minima exists , while more than one local maximum or minimum. Due to curve turn on these point are called local. Hence these point also called stationary points. Maxima and minima
Derivative
The derivative of a function of a single variable at a chosen input value. Derivative is the slope of the tangent line to the graph of the function at that point. Hence derivative of a function y = f(x) of a variable x is a measure of the rate at which the value y of the function changes with respect to the change […]
Derivative of polynomials
Derivative is product of differentiation. Differentiation has applications to nearly all quantitative disciplines. For example, in physics, the derivative of the displacement of a moving body with respect to time is the velocity of the body, and the derivative of velocity with respect to time is acceleration. Therefore differentiation is process Derivative
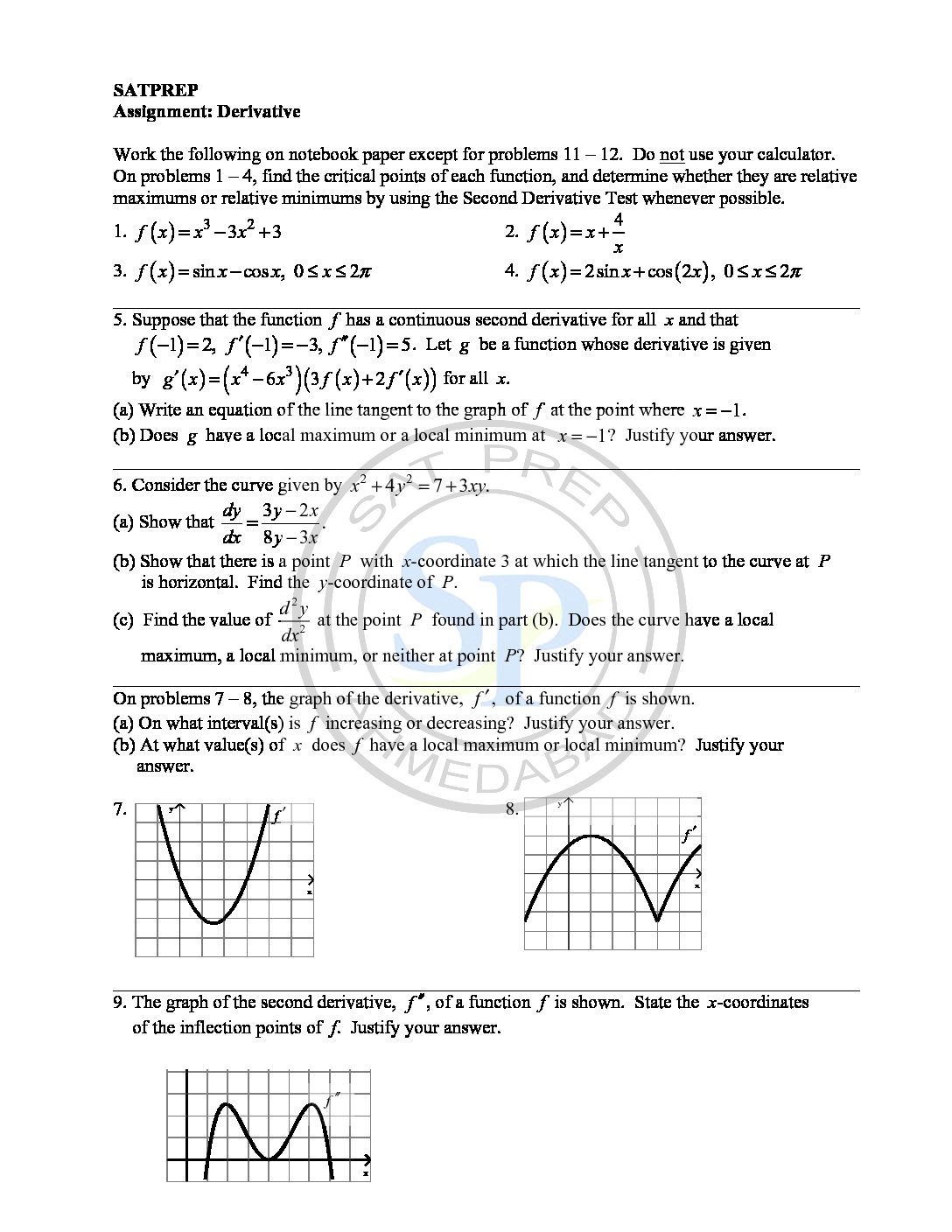
Derivative test
First Derivative Test for Local Extrema. If the derivative changes from positive (increasing function) to negative (decreasing function), the function has a local (relative) maximum at the critical point. Second Derivative Test. 1. If , then has a local minimum at . 2. If , then has a local maximum at . The extremum test gives slightly more general conditions under which […]