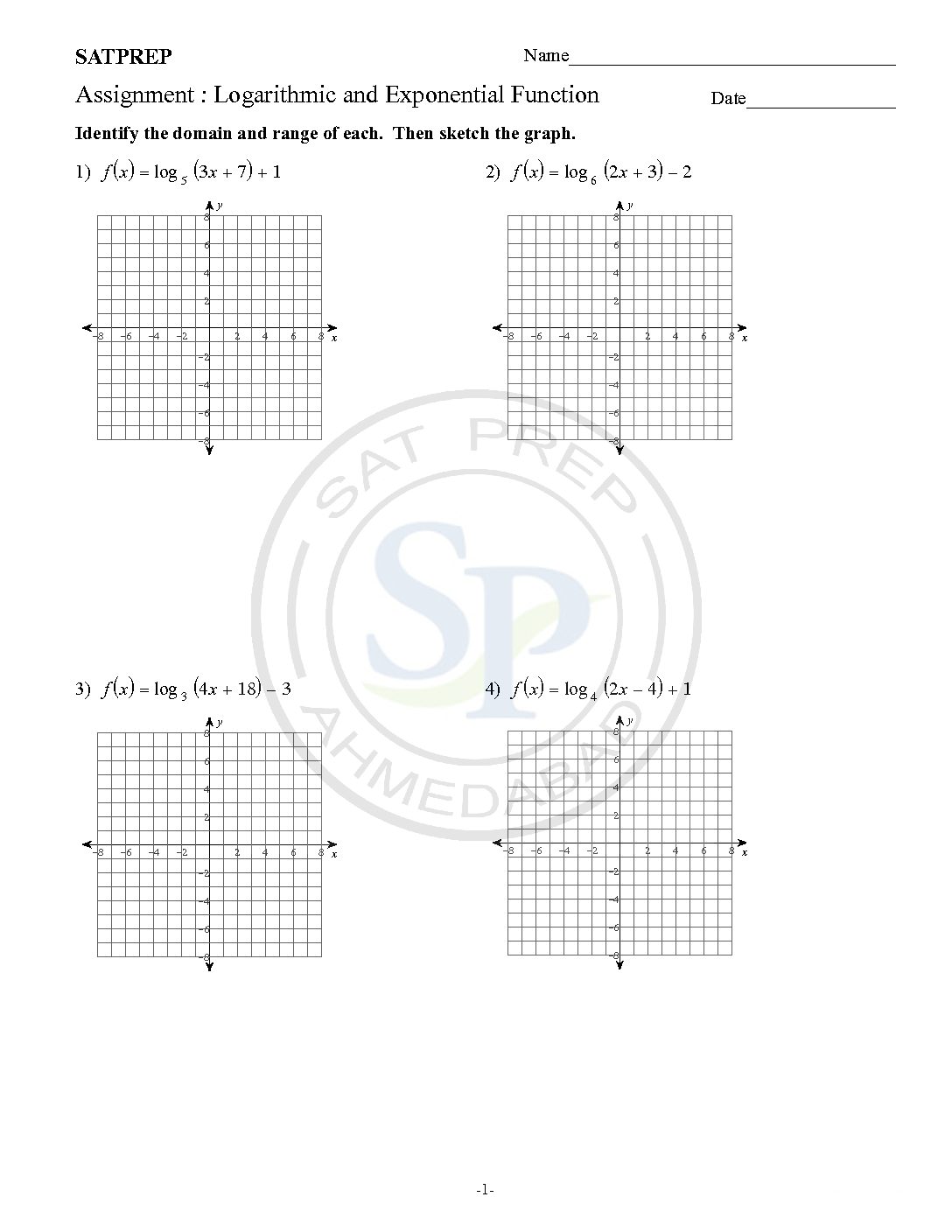
This post is about Exponential and Logarithm function . These function are inverse to each other. Therefore graph function are reflection about line y = x . The questions are to change exponent to log and reverse. Exponential and Logarithm P P
You are browsing archives for
Category: Logarithmic and Exponential Function
Logarithmic Expression
Logarithmic Expressions are simplify by Rules or Laws of Logarithms and solve by inverse of exponentiation. It is expressed by using the abbreviation “log”. Because of different base of number log notation are also different. lg for base 10 , ln for base e . Logarithm quotient rule The logarithm of the division of x and y is the difference of logarithm of x […]
Logarithmic Expression
Solve the logarithmic equation. This problem involves the use of the symbol “ln” instead of “log” to mean logarithm. Logarithmic expression
Logarthmic Equation
Logarithms equation can be solved using the properties of logarithms. So equation either are solve by log or exponent. Because both inverse of each other hence are either way exponent or log.In both apply properties of log or exponent. Also we need to factorised to solve. Logarithmic eq
Logarithmic and exponential Function
The logarithmic function y = logax is defined to be equivalent to the exponential equation x = ay. y = logax only under the following conditions: x = ay, a > 0, and a≠1. Logarithmic functions are the inverses of exponential functions. The inverse of the exponential function y = ax is x = ay. […]
Exponential Equation
Exponential equations are one in which a variable occurs in the exponent, for example, . When both sides of the equation have the same base, the exponents on either side are equal by the property Exponential Equation
Properties of logarithm
Properties of logarithms are use to evaluate or rewrite logarithmic expressions. Product Rule : ln x+ ln y = ln xy Quotient Rule : ln x – ln y = ln xy Power Rule : ln yx = x ln y Properties of logarithm
Exponent and Logarithm inverses
The inverse of the exponential function y = ax is x = ay. The logarithmic function y = logax is defined to be equivalent to the exponential equation x = ay. y = logax only under the following conditions: x = ay, a > 0, and a≠1. It is called the logarithmic function with base […]