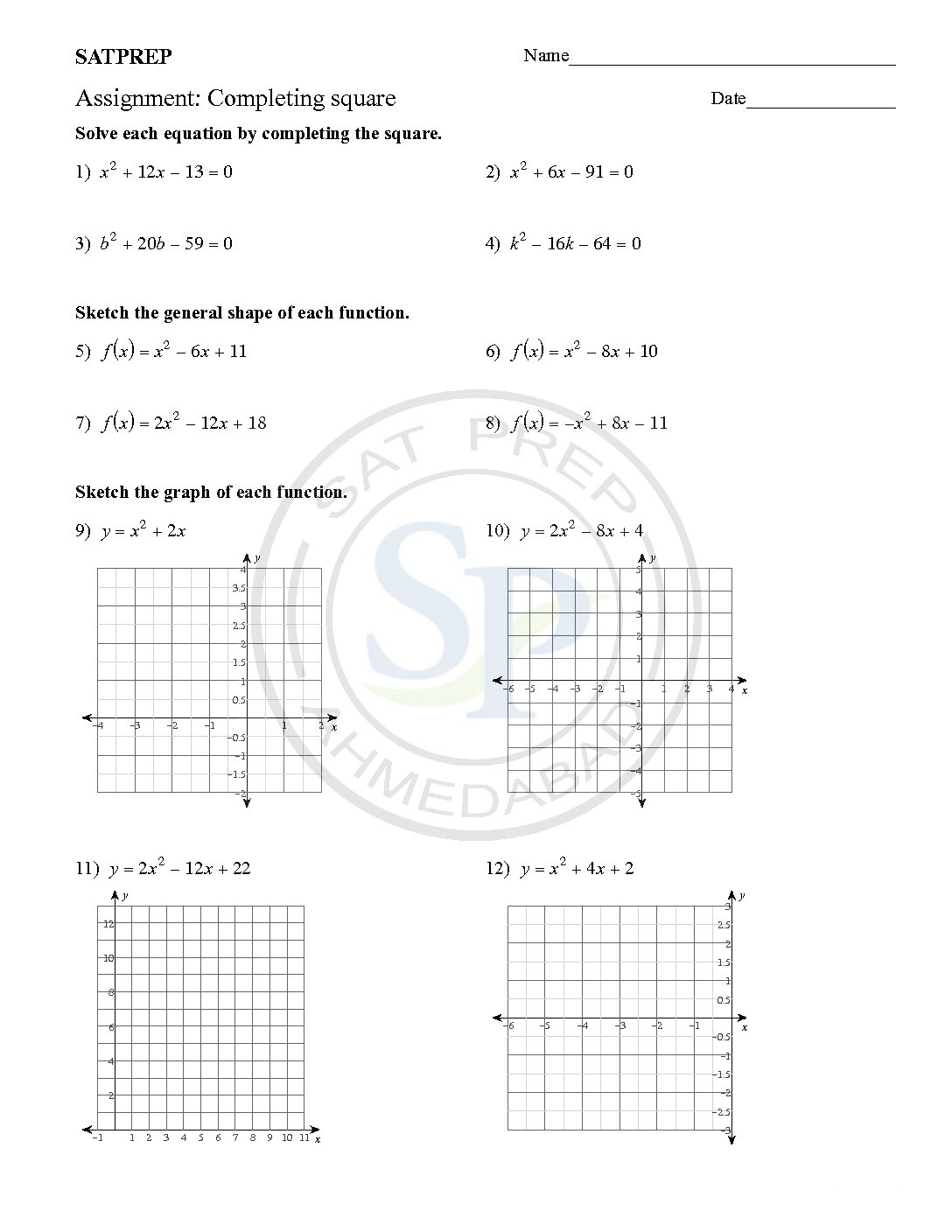
Completing the Square is to solve a quadratic equation by changing the form of the equation so that the left side is a perfect square trinomial. Completing the square is a technique for converting a quadratic polynomial of the form ax2 + bx + c to a(x-b)2+c. Hence this method is used to convert. Similarly […]
You are browsing archives for
Category: Functions
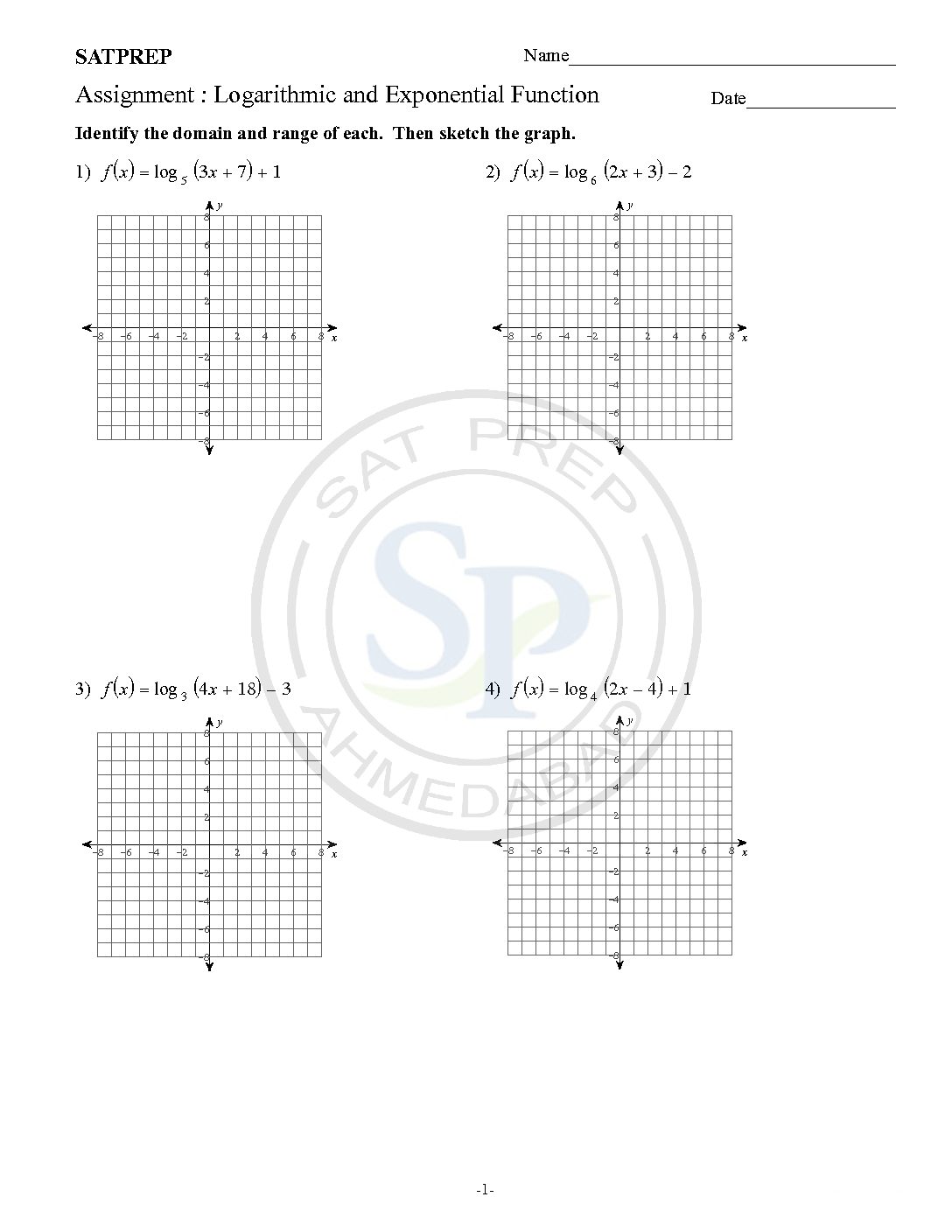
Logarithmic and exponential Function
The logarithmic function y = logax is defined to be equivalent to the exponential equation x = ay. y = logax only under the following conditions: x = ay, a > 0, and a≠1. Logarithmic functions are the inverses of exponential functions. The inverse of the exponential function y = ax is x = ay. […]
Exponential Equation
Exponential equations are one in which a variable occurs in the exponent, for example, . When both sides of the equation have the same base, the exponents on either side are equal by the property Exponential Equation
Properties of logarithm
Properties of logarithms are use to evaluate or rewrite logarithmic expressions. Product Rule : ln x+ ln y = ln xy Quotient Rule : ln x – ln y = ln xy Power Rule : ln yx = x ln y Properties of logarithm
Exponent and Logarithm inverses
The inverse of the exponential function y = ax is x = ay. The logarithmic function y = logax is defined to be equivalent to the exponential equation x = ay. y = logax only under the following conditions: x = ay, a > 0, and a≠1. It is called the logarithmic function with base […]
Quadratics
First of all this post consists of questions of factorisation of quadratics . The method use to find solutions are splitting middle term and another method is formula . We also find the nature of roots of equation. The method is use to find nature is discriminant (D= b2-4ac). Discriminant is also used in formula […]
Completing Square form
Completing form is to solve a quadratic equation by changing the form of the equation so that the left side is a perfect square trinomial. Completing the square is a technique for converting a quadratic polynomial of the form ax2 + bx + c to a(x-b)2+c. Hence this method is used to convert. Similarly it use to […]
Function
A functions f(x) tells you what to do with the input, but, to be completely defined, function also need to know what type of input is permitted to go into the function. Function
Curve sketching
Curve Sketching. If f (-x) = -f (x) for all x in the domain, then f is odd and symmetric about the origin. d) Asymptotes: Find the asymptotes of the function using the methods described above. First attempt to find the vertical and horizontal asymptotes of the function. Curve sketching
Curve Sketching -2
the sketching of curve though coordinate of turning and axes intercepts . So equation of the curve is given. Curve sketching