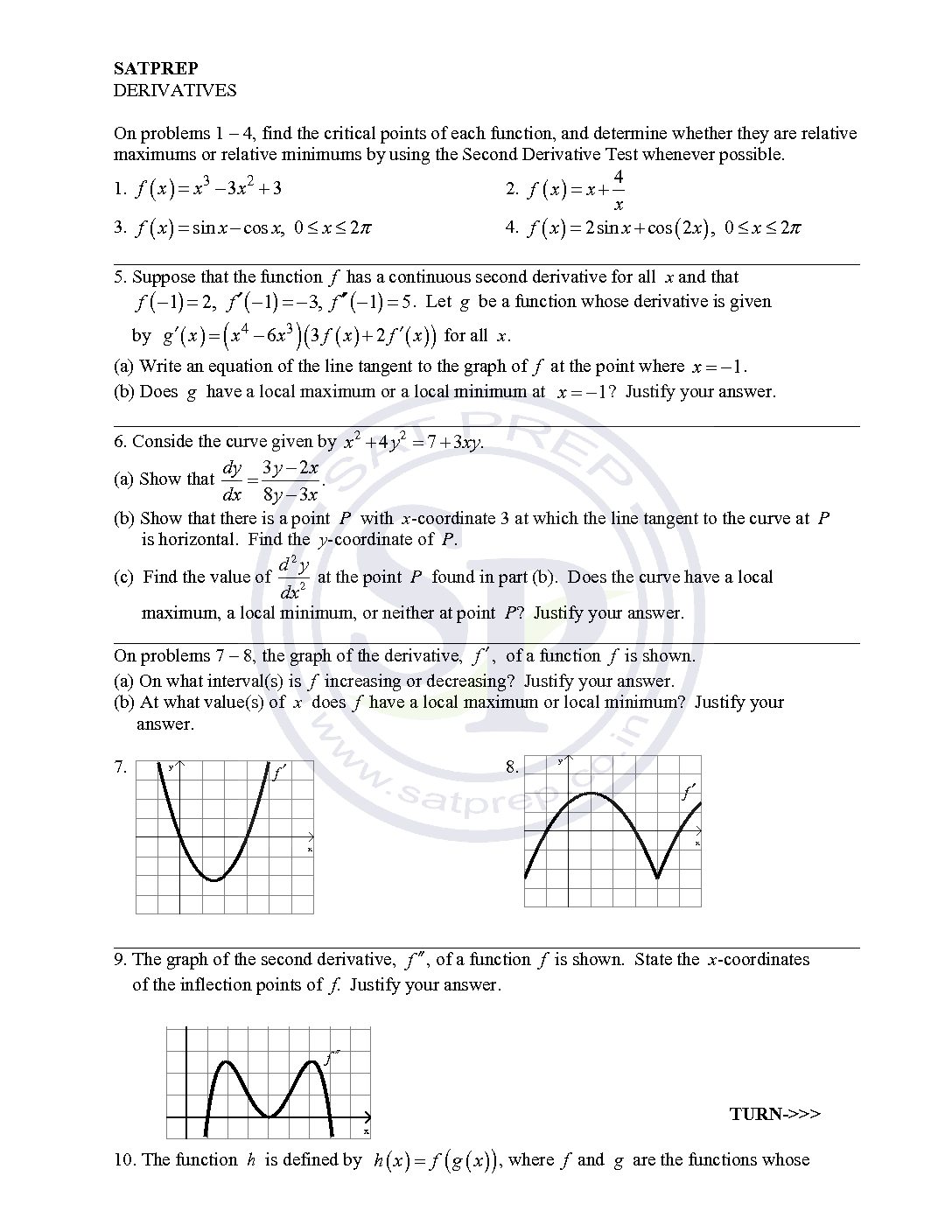
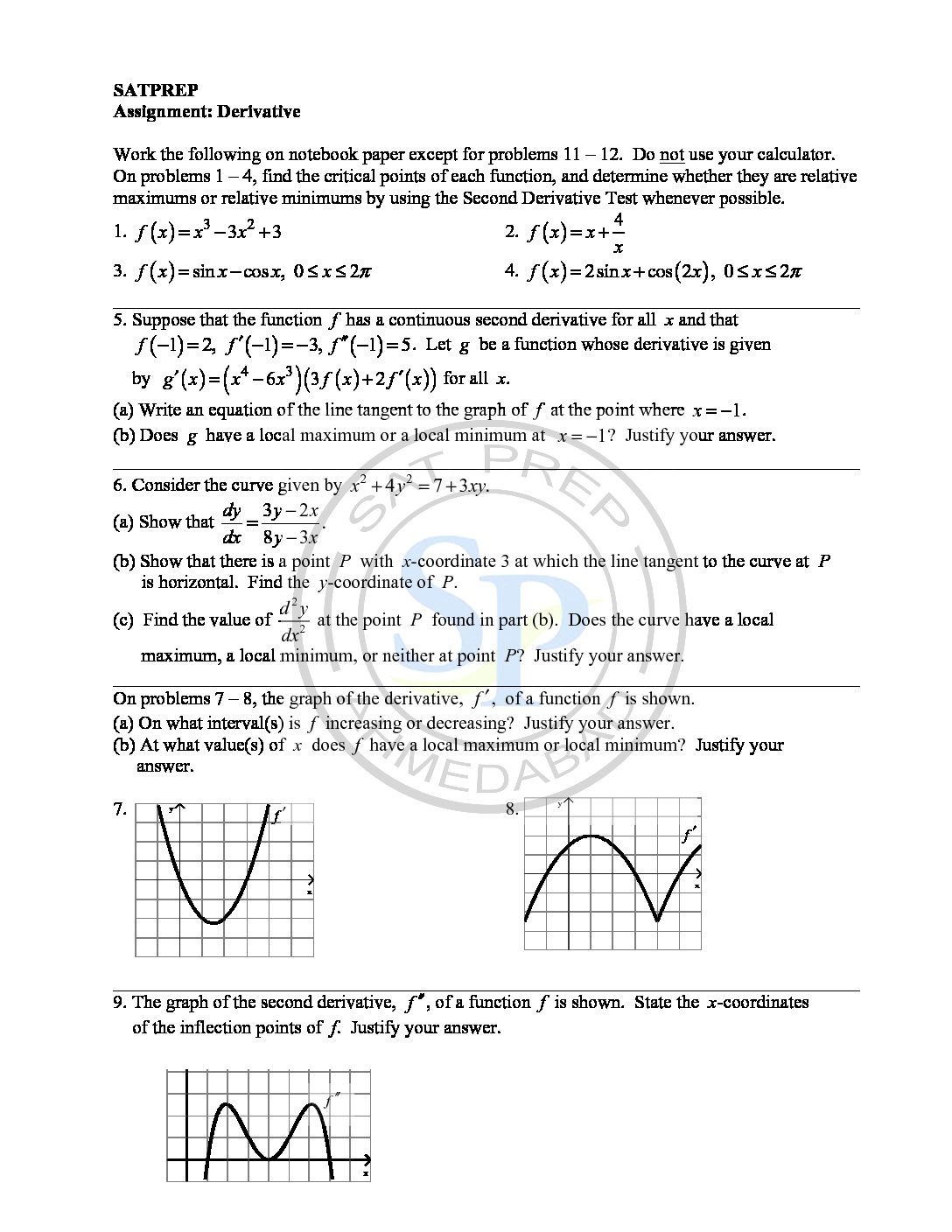
Differentiable functions of one variable is a function whose derivative exists at each point in its domain. Also function is differentiable at a point if it has a derivative there. Therefore function also continuous in given domain. Differentiable_function
You are browsing archives for
Category: Applications of Derivative
Equation of tangent and normal of transc...
The Equation of Tangents and Normals, If you differentiate the equation of a curve, you will get a formula for the gradient of the curve. Are you working to find the equation of a tangent line (or normal line) in Calculus? The derivative of a function at a point is the slope of the tangent line at this point. The normal line is defined as the line that is perpendicular to […]
Properties of curve
derivative find (in general) points of inflection on the curve. If the graph of a function were a road map, these are the points on the curve where, instantaneously. Also use to find Maxima and minima. Properties of curve
Equation of Tangent and Normal
A tangent to a curves are a line that touches the curve at one point and has the same slope as the curve at that point. A normal to a curve is a line perpendicular to a tangent to the curve. Tangent and normal
Kinematics
Kinematic is the branch of classical mechanics. describes the motion of points, objects and systems of groups of objects, without reference to the causes of motion. The symbol a stands for the acceleration of the object. And the symbol v stands for the instantaneous velocity of the object. The derivative of displacement with time is velocity […]
Equation of Tangent and Normal
Tangents to a curve are a line that touches the curve at one point and has the same slope as the curve at that point. A normal to a curve is a line perpendicular to a tangent to the curve. Tangent and Normal
Point of inflection
Inflection Point. An inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. Inflection points may be stationary points, but are not local maxima or local minima. For example, for the curve plotted above, the point is an inflection point. Point of infection
Differentiation of polynomial
Differentiation is process of getting derivative. Differentiation has applications to nearly all quantitative disciplines. For example, in physics, the derivative of the displacement of a moving body with respect to time is the velocity of the body, and the derivative of velocity with respect to time is acceleration. Similarly in chemistry as well as Economics also derivative
Derivative
The derivative of a function of a single variable at a chosen input value. Derivative is the slope of the tangent line to the graph of the function at that point. Hence derivative of a function y = f(x) of a variable x is a measure of the rate at which the value y of the function changes with respect to the change […]
Derivative of polynomials
Derivative is product of differentiation. Differentiation has applications to nearly all quantitative disciplines. For example, in physics, the derivative of the displacement of a moving body with respect to time is the velocity of the body, and the derivative of velocity with respect to time is acceleration. Therefore differentiation is process Derivative