In calculus, a methods of implicit differentiation, Makes use of the chain rule to differentiate implicitly defined functions. To differentiate an implicit function y ( x ), defined by an equation R ( x, y) = 0, it is not generally possible to solve it explicitly for y and then differentiate. The derivatives of inverse trig functions we’ll need the formula from the last section […]
You are browsing archives for
Category: Derivatives
Composite Function
Composite functions are defined as one function defined inside another function. Like ff(x)) or f(g(x)) etc. Another function composition is an operation that takes two functions f and g and produces a function h such that h(x) = g(f(x)) Composite function
Point of inflection
Inflection Point. An inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. Inflection points may be stationary points, but are not local maxima or local minima. For example, for the curve plotted above, the point is an inflection point. Point of infection
Quadratics
First of all this post consists of questions of factorisation of quadratics . The method use to find solutions are splitting middle term and another method is formula . We also find the nature of roots of equation. The method is use to find nature is discriminant (D= b2-4ac). Discriminant is also used in formula […]
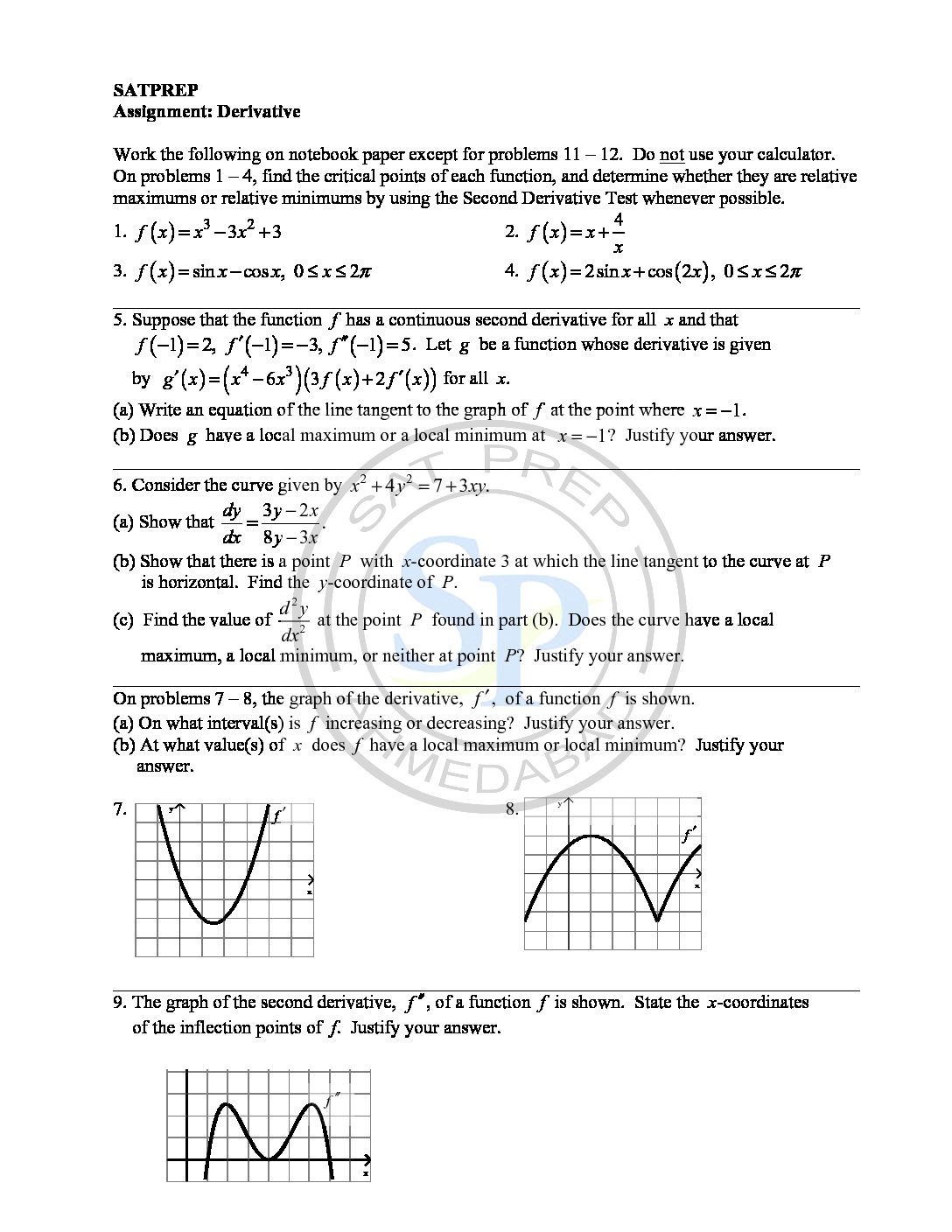
Differentiation of polynomial
Differentiation is process of getting derivative. Differentiation has applications to nearly all quantitative disciplines. For example, in physics, the derivative of the displacement of a moving body with respect to time is the velocity of the body, and the derivative of velocity with respect to time is acceleration. Similarly in chemistry as well as Economics also derivative
Derivative
The derivative of a function of a single variable at a chosen input value. Derivative is the slope of the tangent line to the graph of the function at that point. Hence derivative of a function y = f(x) of a variable x is a measure of the rate at which the value y of the function changes with respect to the change […]
Curve Sketching -2
the sketching of curve though coordinate of turning and axes intercepts . So equation of the curve is given. Curve sketching
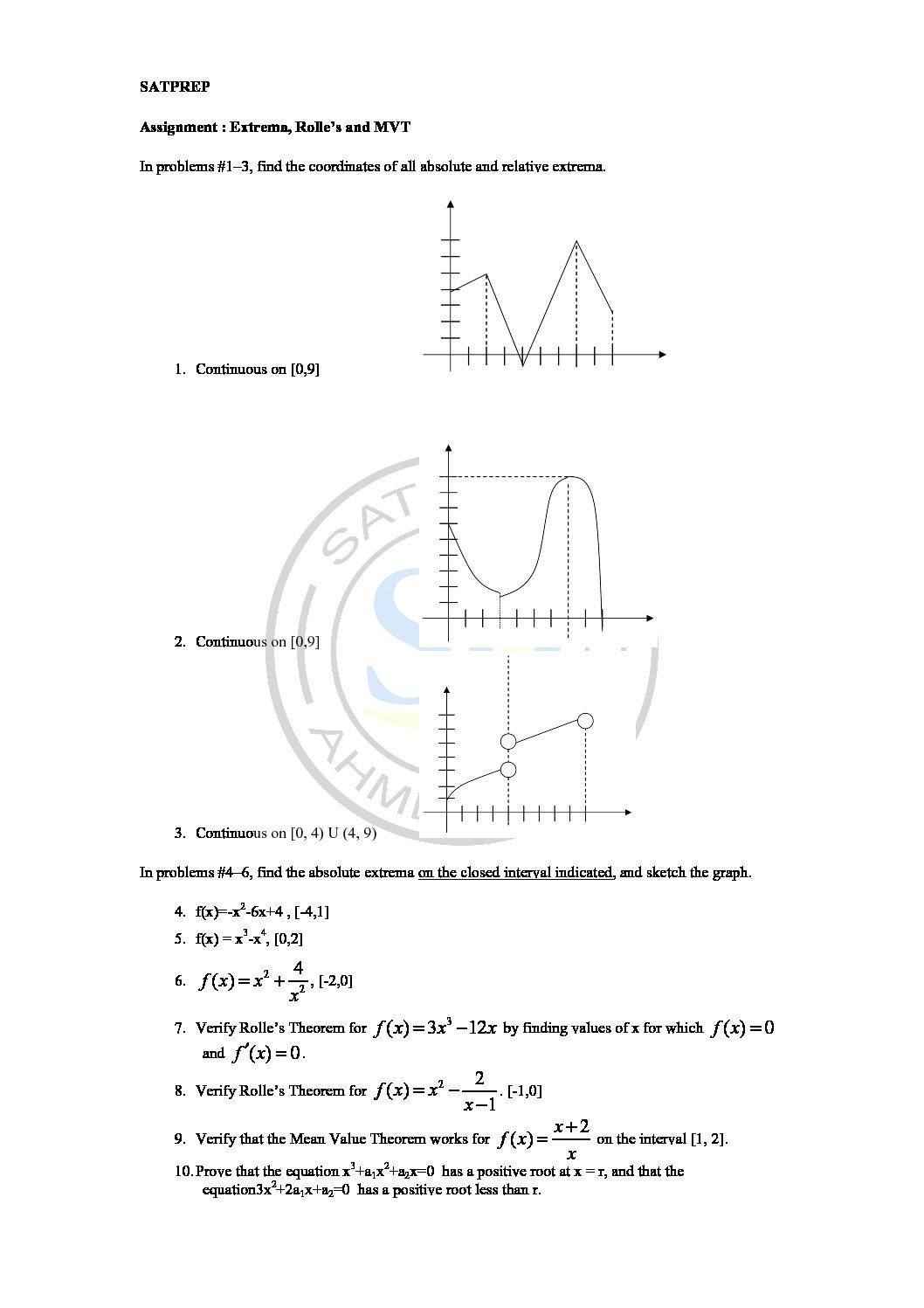
Extrema, Rolle’s and MVT
MVT. Theorem states that if a function f is continuous on the closed interval [a,b] and differentiable on the open interval (a,b), then there exists a point c in the interval (a,b) such that f'(c) is equal to the function’s average rate of change over [a,b]. Mean value theorem
Rolle’s and MVT
Rolle’s Theorem. Then there is a number c such that a<c<b and f′(c)=0. Or, in other words f(x) has a critical point in (a,b). To see the proof of Rolle’s Theorem see the Proofs From Derivative Applications . Roll’s theorem
Derivative of polynomials
Derivative is product of differentiation. Differentiation has applications to nearly all quantitative disciplines. For example, in physics, the derivative of the displacement of a moving body with respect to time is the velocity of the body, and the derivative of velocity with respect to time is acceleration. Therefore differentiation is process Derivative