nth degree polynomial with real coefficients has precisely n complex roots . Hence when all root cannot be real. Complex root with Polynomial
You are browsing archives for
Category: Pure Maths
Arithmetics of complex no
imaginary number is any number of the form a + bi where a and b are real numbers. Addition and Subtraction of complex numbers is to add or subtract real parts and the imaginary parts. complex no
Vectors and scalar product
Scalar product of two vectors is multiply and obtain a scalar quantity. It represent on ‘dot’. Another name is dot product. vector has magnitude and direction. It start from one point to another point. The length of vector is called magnitude. Scalar product and vector
Vector and Scalar product.
vector has magnitude and direction. It start from one point to another point. The length of vector is called magnitude. The scalar product of two vectors is multiply and obtain a scalar quantity. It represent on ‘dot’. Another name is dot product. Vector and scalar product
Polynomial
The polynomials are an expression involving a sum of powers in one or more variables multiplied by coefficients and constant. Polynomial linear , quadratic etc as per value of n=1, n = 2 etc . We can graph the polynomial for finding solution. Another polynomial is also use for curve as well as st. line. As […]
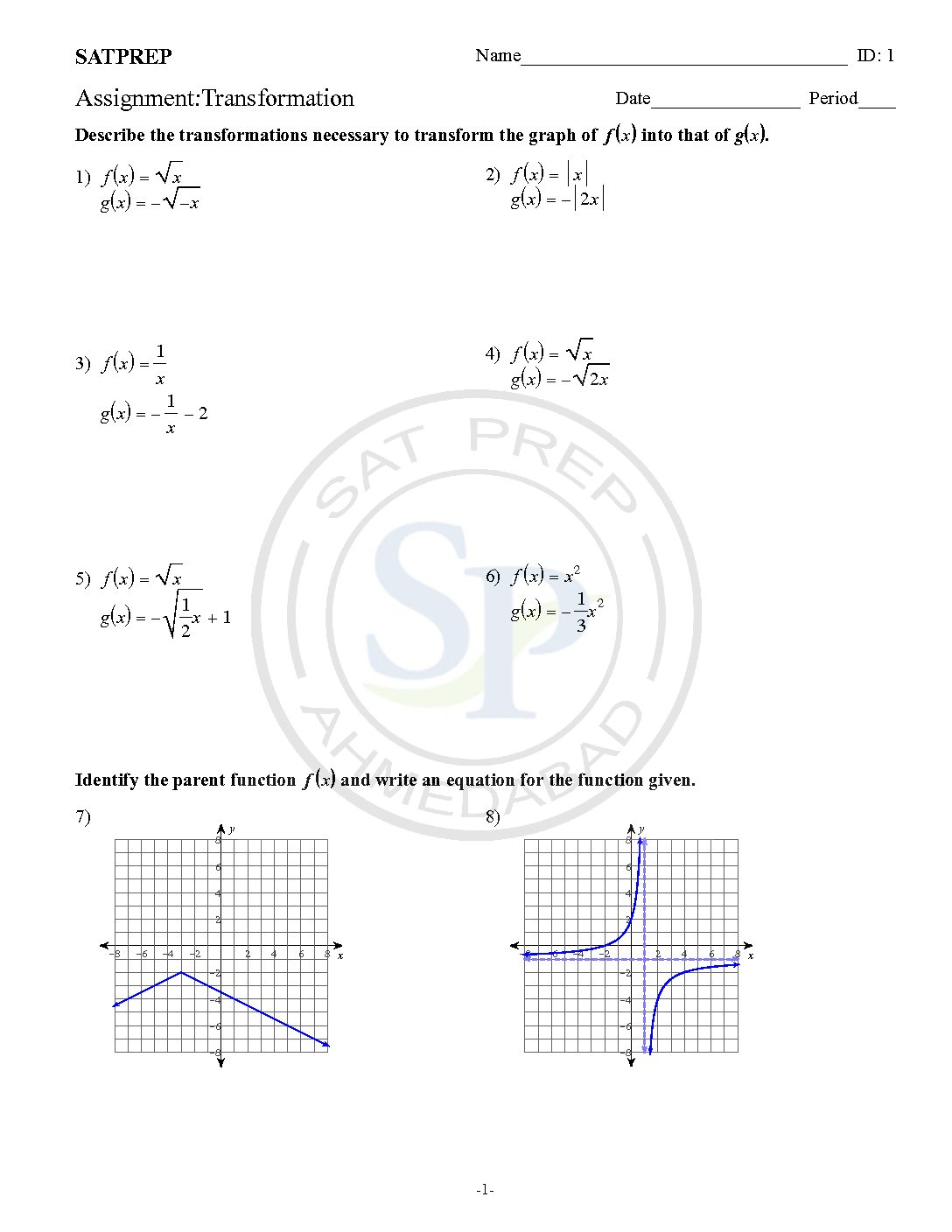
Transformation
In this post question are from transformation of function. It basically deals with translation of functions through vector . Also it deal with reflection . Transformation
Co-ordinate geometry -2
Ordered pair of numbers also known as coordinates. Hence manipulation of coordinate such as Determine the distance between these points. Find the equation, midpoint, and slope of the line segment. Determine if the given lines are perpendicular or parallel. Also deal with graphic representation. Coordinate geometry
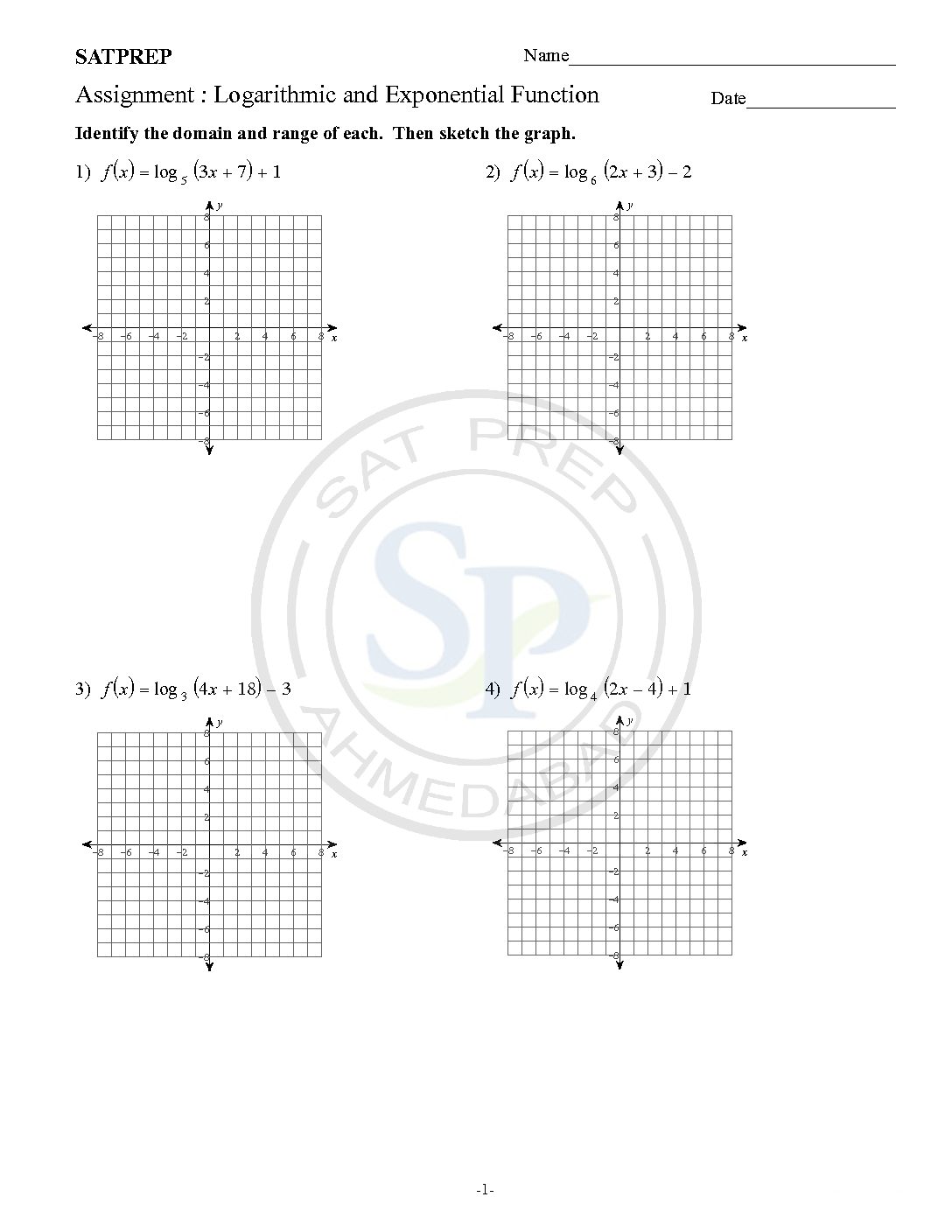
Logarithmic and exponential Function
The logarithmic function y = logax is defined to be equivalent to the exponential equation x = ay. y = logax only under the following conditions: x = ay, a > 0, and a≠1. Logarithmic functions are the inverses of exponential functions. The inverse of the exponential function y = ax is x = ay. […]
Properties of logarithm
Properties of logarithms are use to evaluate or rewrite logarithmic expressions. Product Rule : ln x+ ln y = ln xy Quotient Rule : ln x – ln y = ln xy Power Rule : ln yx = x ln y Properties of logarithm
Exponent and Logarithm inverses
The inverse of the exponential function y = ax is x = ay. The logarithmic function y = logax is defined to be equivalent to the exponential equation x = ay. y = logax only under the following conditions: x = ay, a > 0, and a≠1. It is called the logarithmic function with base […]