to calculate Further Probabilities. Further Probability. An event ( E) is a subset of the sample space. That is, an event is a subset of all possible outcomes. We refer to this subset of outcomes as favourable outcomes. Further Probability
You are browsing archives for
Category: Cambridge Maths AS
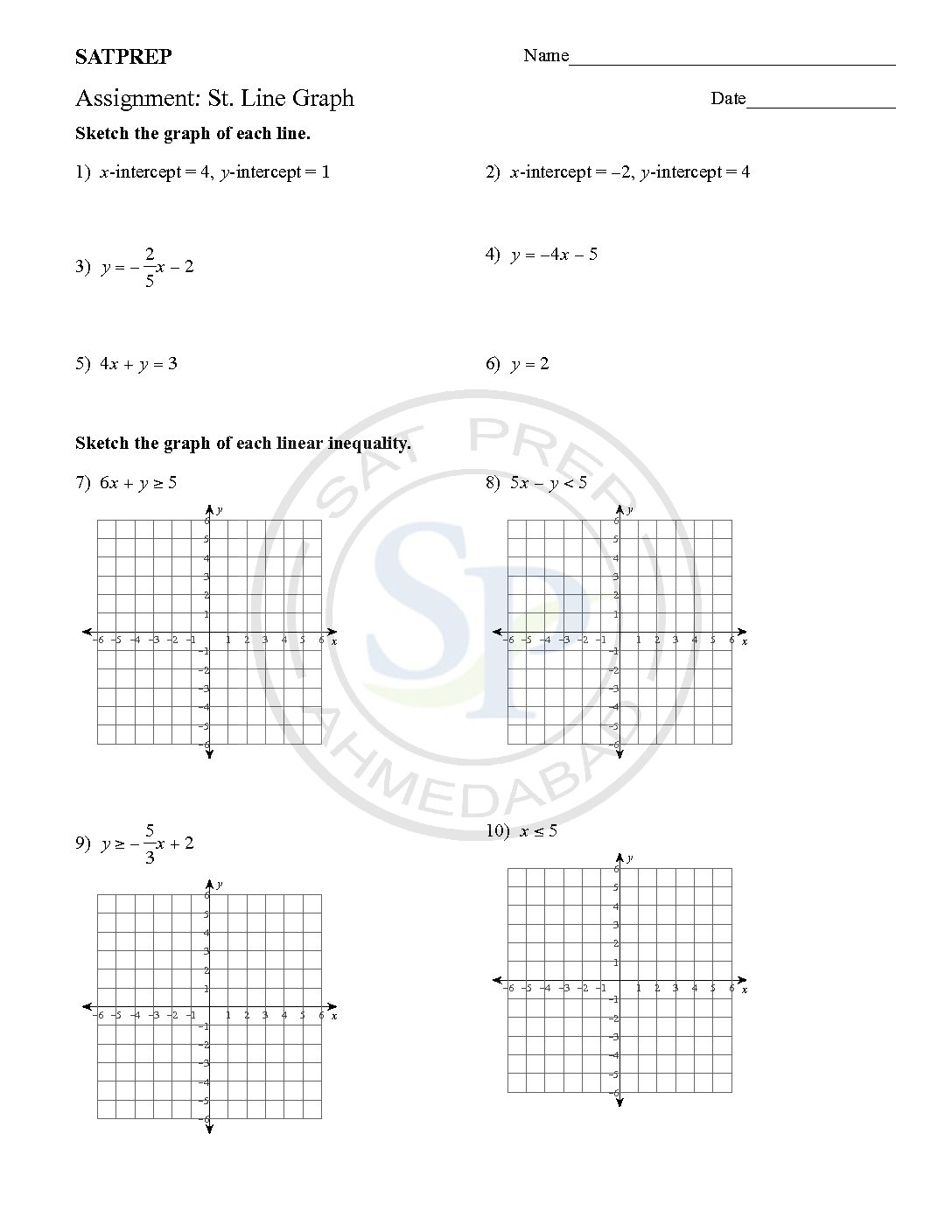
Straight line
Simultaneous Equation
The simultaneous equations are solve by the elimination. These equations are also solve by substitution as well as graphic method. Due to variable solution give coordinate. Simultaneous eq
Parabola
Vertex of a parabola is at the ‘origin’ and the axis of symmetry is along the x or y-axis, then the equation of the parabola is the simplest. So that its vertex is (h,k) and its axis of symmetry is parallel to the x-axis, it has an equation of (y – k)2= 4p (x – […]
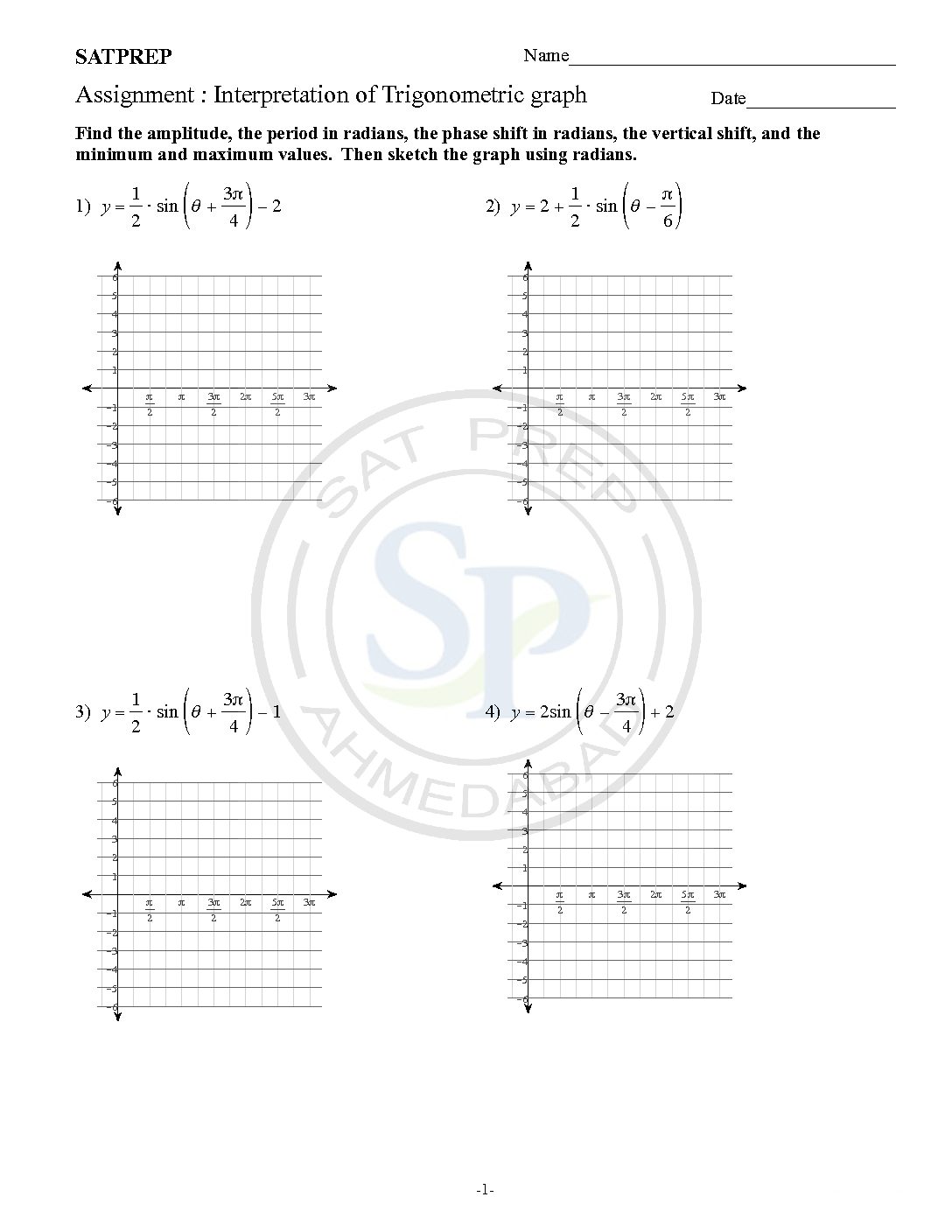
Interpretation of trigonometric graph
Sound waves travel in a repeating wave pattern. This represent graphically by sine and cosine functions. As trigonometric function is periodic therefore it use for sound wave. Similarly we use in wheel also for model function, because of rotation of wheel. Also use of periodic conditions. trigonometric function
Trigonometric Equation (Radian)
Trigonometric Equation involve one or more trigonometric ratios of unknown angles. Due to difference unit of angle , hence it gives angle in different form. Similarly it give value in radian. Trigonometric equation
Trigonometric Equation(Degree)
Trigonometric Equations involve one or more trigonometric ratios of unknown angles. Due to difference unit of angle , hence it gives angle in two different form. Similarly it give value in degree. Trigonometric Equation
Trigonometric identity
Trig identity is equations that are true for Right Angled Triangles. D1: sin 2A+ cos 2A=1 D2: 1+ tan 2A= sec 2A D3: 1+ cot 2A= csc 2A Hence trigonometric identities are prove by above D1,D2 and D3. Similarly also using reciprocal identity. Trigonometric Identity
Permutation and combination-2
Permutation and Combination is a very important topic of mathematics as well as the quantitative aptitude section. In permutation we arrange object while in combination we select items. Permutation and combination
Permutation and combination-1
Combination and permutation and is a very important topic of mathematics as well as the quantitative aptitude section. In permutation we arrange object while in combination we select items. Combination and Permutation