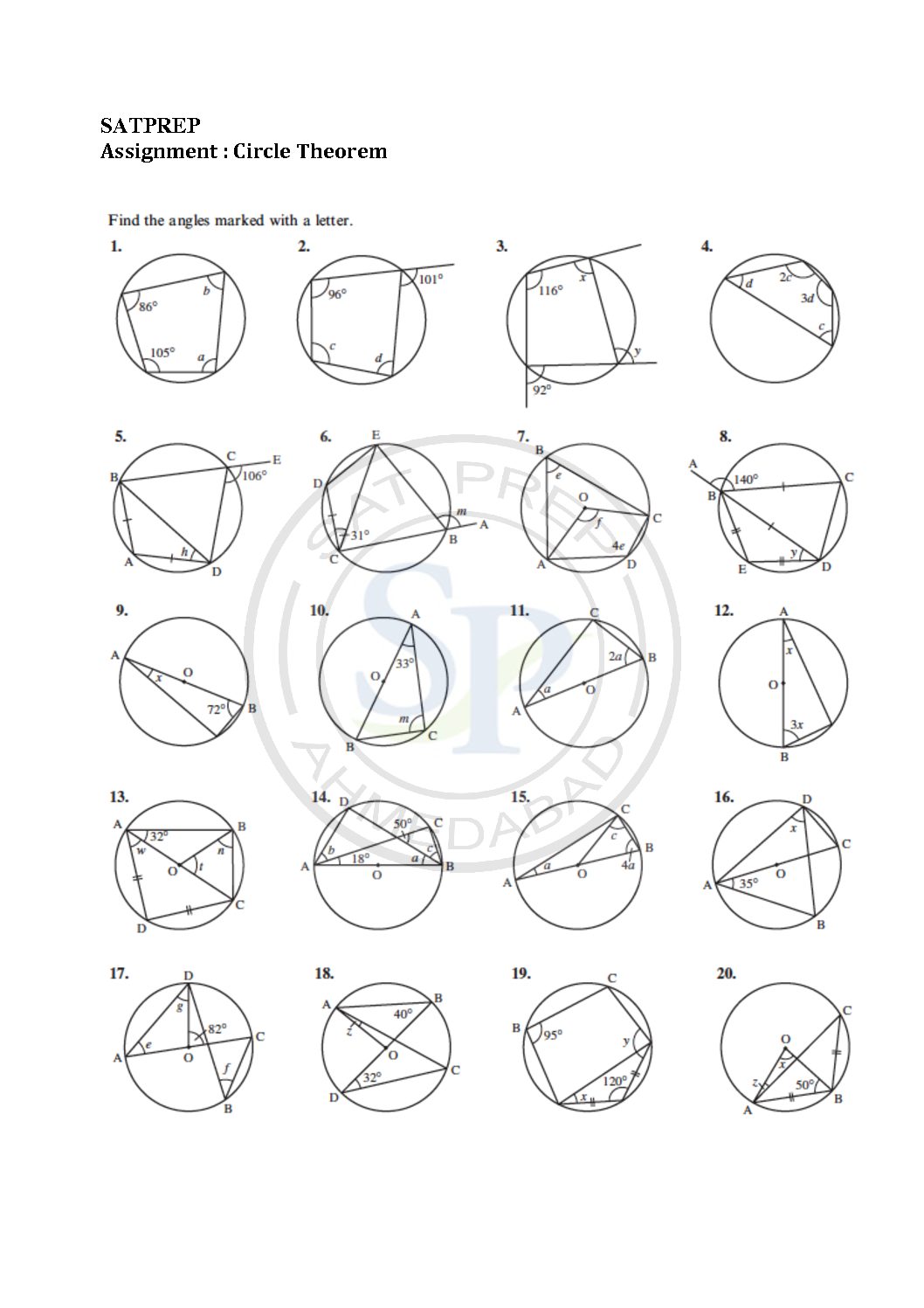
This post about is the Circle theorems. Formulas for the radius of a circle, the diameter of a circle, the circumference (perimeter) of a circle. Therefore It also include the length of chord of a circle. Because of length of chord angle also varies. Similarly other properties also involve. Explore, prove, and apply important properties of circles that have […]
You are browsing archives for
Category: Trignometry and Circular Function
Double angle trigonometric equation
Double angle equations are allowing the expression of trigonometric functions of angles equal to 2u in terms of u. The double angle formulas can simplify the functions and gives ease to perform more complex calculations. The double angle formulas are useful for finding the values of unknown trigonometric functions. Therefore in double angle equation we need to consider two rotation. […]
A Double angles identity
A Double angles identity is written2θ, for example, as sin 2θ, cos 2α, or tan 2x, where 2θ, 2α, and 2x. The angle measures and the assumption is that you mean sin(2θ), cos(2α), or tan(2x). Because tangent is equal to the ratio of sine and cosine . Therefor its identity comes from their double-angle identities. double angle identity
Double Angle trigonometric Identity
A Double angles identity is written2θ, for example, as sin 2θ, cos 2α, or tan 2x, where 2θ, 2α, and 2x. The angle measures and the assumption is that you mean sin(2θ), cos(2α), or tan(2x). Because tangent is equal to the ratio of sine and cosine . Therefor its identity comes from their double-angle identities. Double angle
Trigonometric equations
Trigonometric equations use both the reference angles and trigonometric identities The general method of solving an equation is to convert it into the form of one ratio only. Hence, we can obtain solutions. Trigonometric Equation
Trigonometric Identity
The trigonometric identity showing that the identity is always true, no matter what value of x or θ is used. Because it has to hold true for all values of x, we cannot simply substitute in a few values of x to “show” that they are equal. We have to use logical steps to show […]
Trigonometric Identity
trigonometry identities showing that the identity is always true, no matter what value of x or θ is used. Because it has to hold true for all values of x, we cannot simply substitute in a few values of x to “show” that they are equal. We have to use logical steps to show that one […]
Product to Sum
Product‐Sum and Sum‐Product Identities. The process of converting products into sums can make a difference . Integrate \( \int \! \sin 3x \cos 4x \, \mathrm{d}x.\) This problem may seem tough at first, but after using the product-to-sum trigonometric formula, this integral very quickly changes into a standard form . Converting a sum of trig functions into a product. Write as and then […]
Linear trigonometric equation
Linear Trigonometric equations are either linear or quadratic in nature. To find the angle value(s) that satisfy the given equation. Because it is linear trigonometric eq. hence it has two roots. Linear trigonometric eq
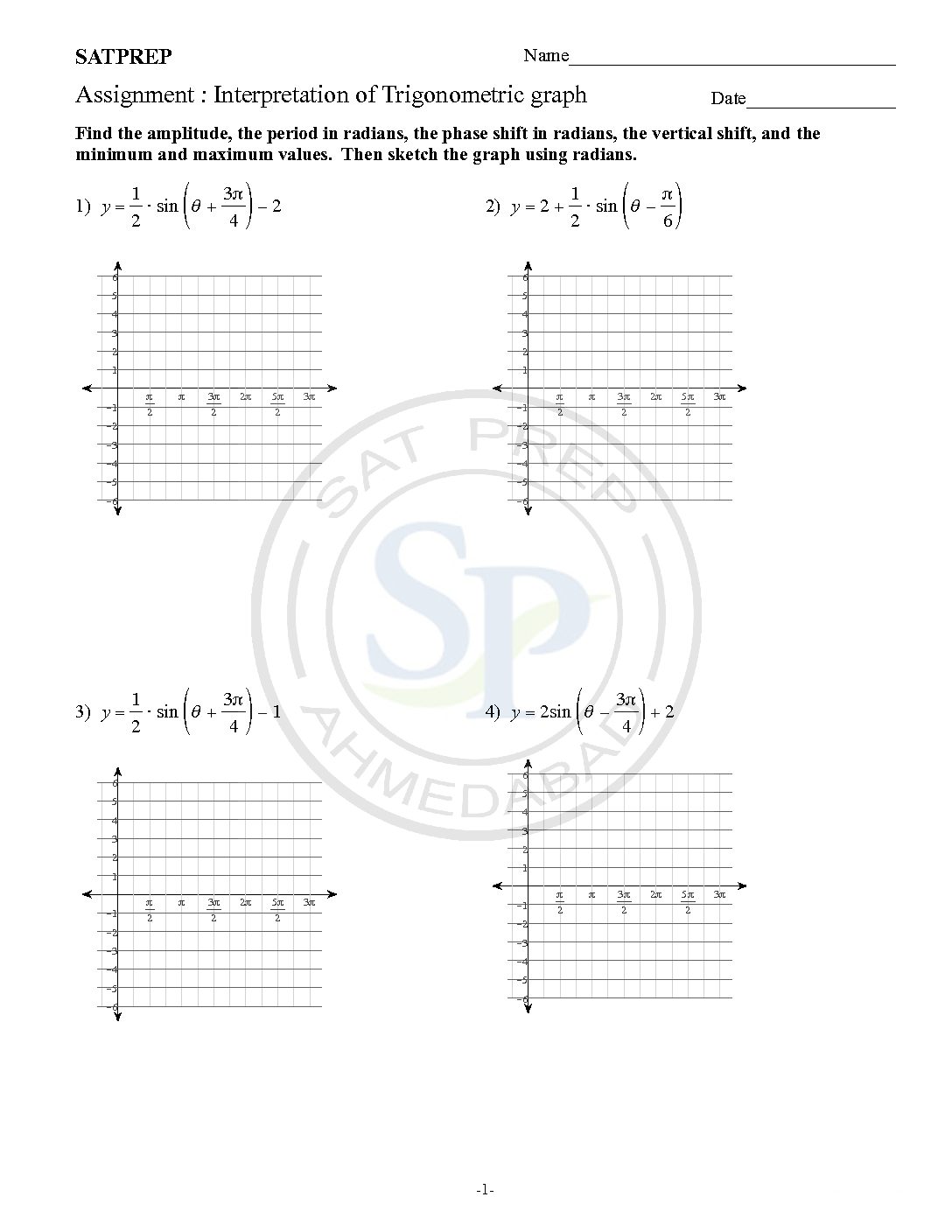
Interpretation of trigonometric graph
Sound waves travel in a repeating wave pattern. This represent graphically by sine and cosine functions. As trigonometric function is periodic therefore it use for sound wave. Similarly we use in wheel also for model function, because of rotation of wheel. Also use of periodic conditions. trigonometric function