In this post table containing values of differentiable functions f (x), g(x) and their derivatives. Use the table data and the rules of differentiation to solve each problem. Derivative Rules. The Derivative tells us the slope of a function at any point. Therefore rules we can follow to find many derivatives. Further more it is derivate of function. All above it is application of derivative Differentiation table rule
You are browsing archives for
Category: mc_c_d
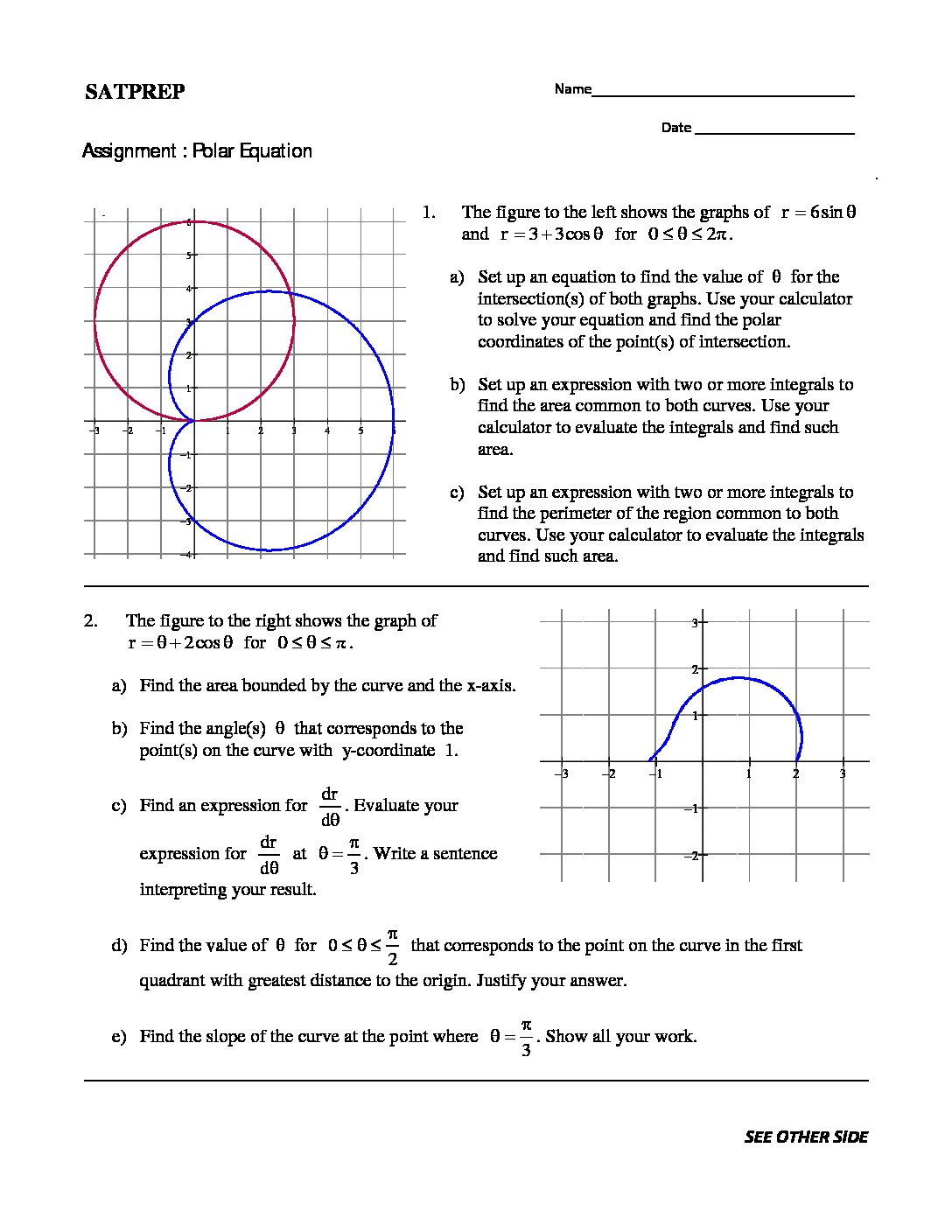
Derivative of polar equation
This post is about derivatives of Polar Equations. Because of polar equation, Polar equation like parametric equations of the curve where the angle θ is parameter. As well as equations have parameter (r,θ). For this polar equation, the parametric equations are x ( θ) = cos θ and y ( θ) = sin θ. Therefore, the derivative is which […]
Derivative of Polar Equation
This post is about derivatives of Polar Equations. Because of polar equation, Polar equation like parametric equations of the curve where the angle θ is parameter. As well as equations have parameter (r,θ). For this polar equation, the parametric equations are x ( θ) = cos θ and y ( θ) = sin θ. Therefore, the derivative is which […]
Differentiation and Integration
First of all differentiation and Integration are process of calculus. Due to differentiation we get derivative, while integration of derivative we get function back. Integration also called derivative. Differentiation and Integration
Derivative of implicit and inverse trigo...
In calculus, a methods of implicit differentiation, Makes use of the chain rule to differentiate implicitly defined functions. To differentiate an implicit function y ( x ), defined by an equation R ( x, y) = 0, it is not generally possible to solve it explicitly for y and then differentiate. The derivatives of inverse trig functions we’ll need the formula from the last section […]
Tangent and normal
Tangents and Normals to a curve are a line that touches the curve at one point and has the same slope as the curve at that point. A normal to a curve is a line perpendicular to a tangent to the curve. Tangent and normal
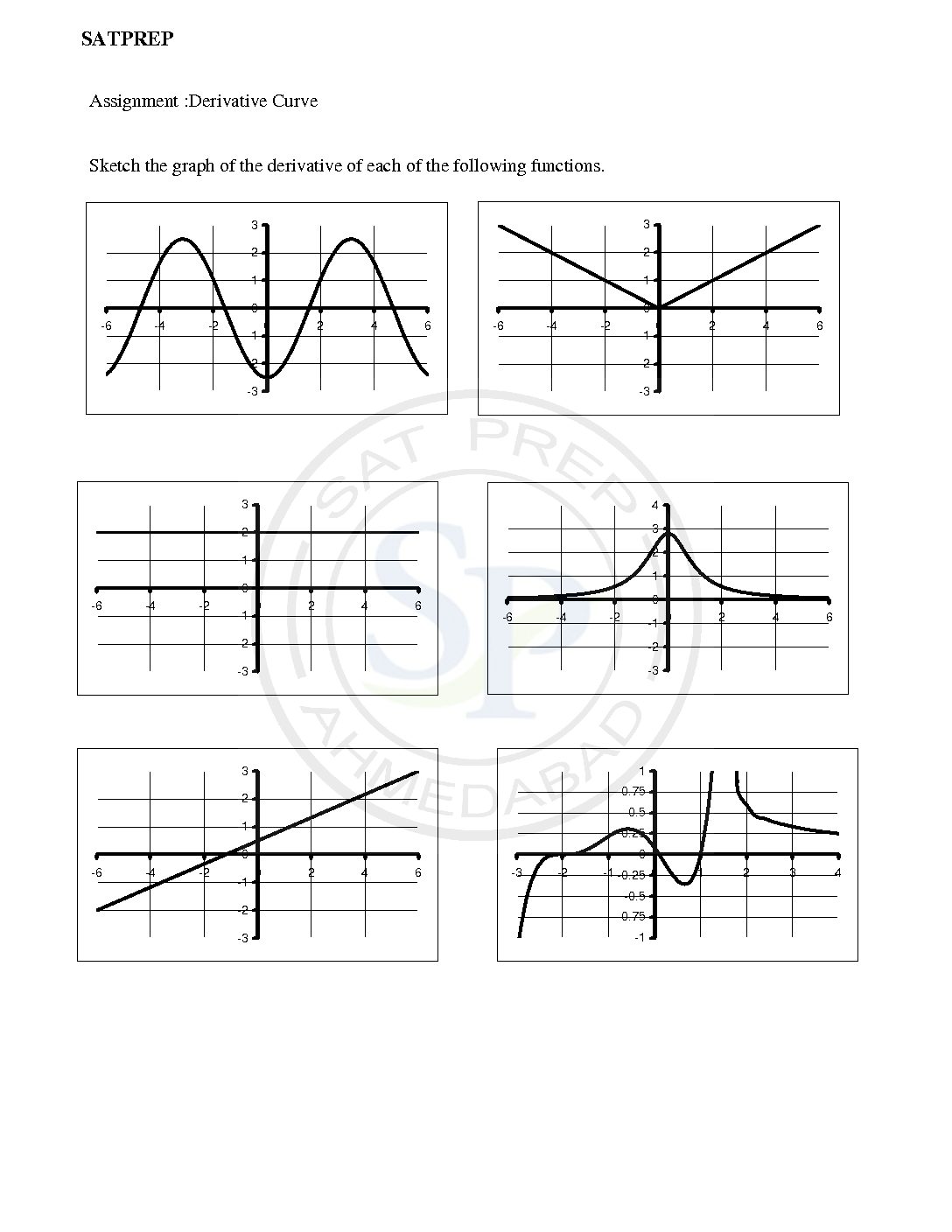
Derivative curve
This post about sketching of derivative curve from function curve. Given the graph of a function y = f(x) a standard approach is to identity intervals over which the graph is increasing, another intervals over which it is decreasing, and points at which the tangent line is horizontal. Derivative curve
Optmization-3
Process of optimisation means optimal value of function at turning point (maximum or minimum ) value of the curve. Therefore second derivative use to find greatest or least value . Also it show greatest value. Optimization
Derivative
First derivative for stationary point of the curve. If the derivative changes from positive (increasing function) to negative (decreasing function), the function has a local (relative) maximum at the critical point. Second Derivative 1. If , then has a local minimum at . 2. If , then has a local maximum at . The extremum test gives slightly more […]
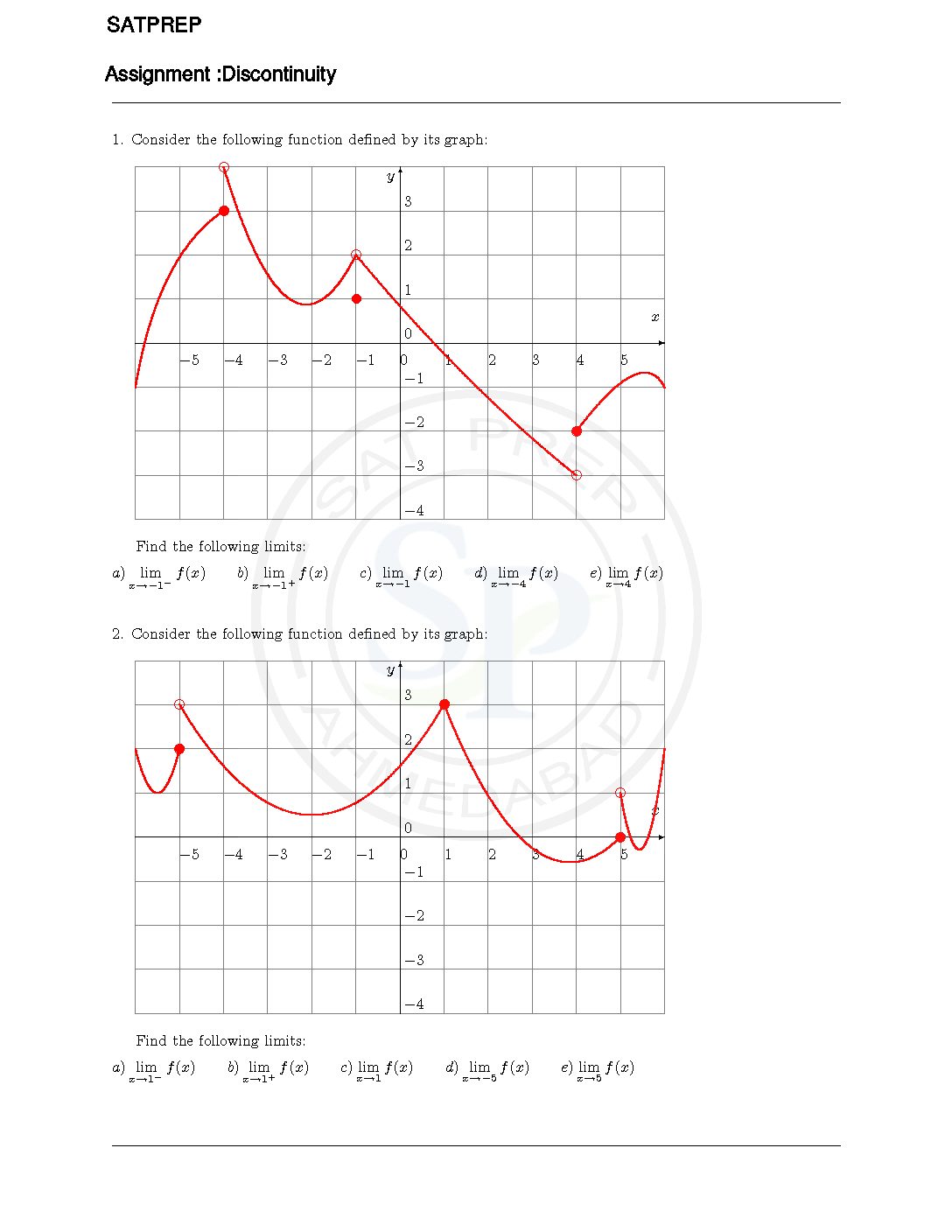
Discontinuity and Limit
An infinite discontinuity exists when one of the one-sided limits of the function is infinite. If the two one-sided limits have the same value, then the two-sided limit will also exist. Discontinunity and limit