This post about equation of lines . Eq. of line is part of coordinate geometry. Equation of line
You are browsing archives for
Category: SAT Math
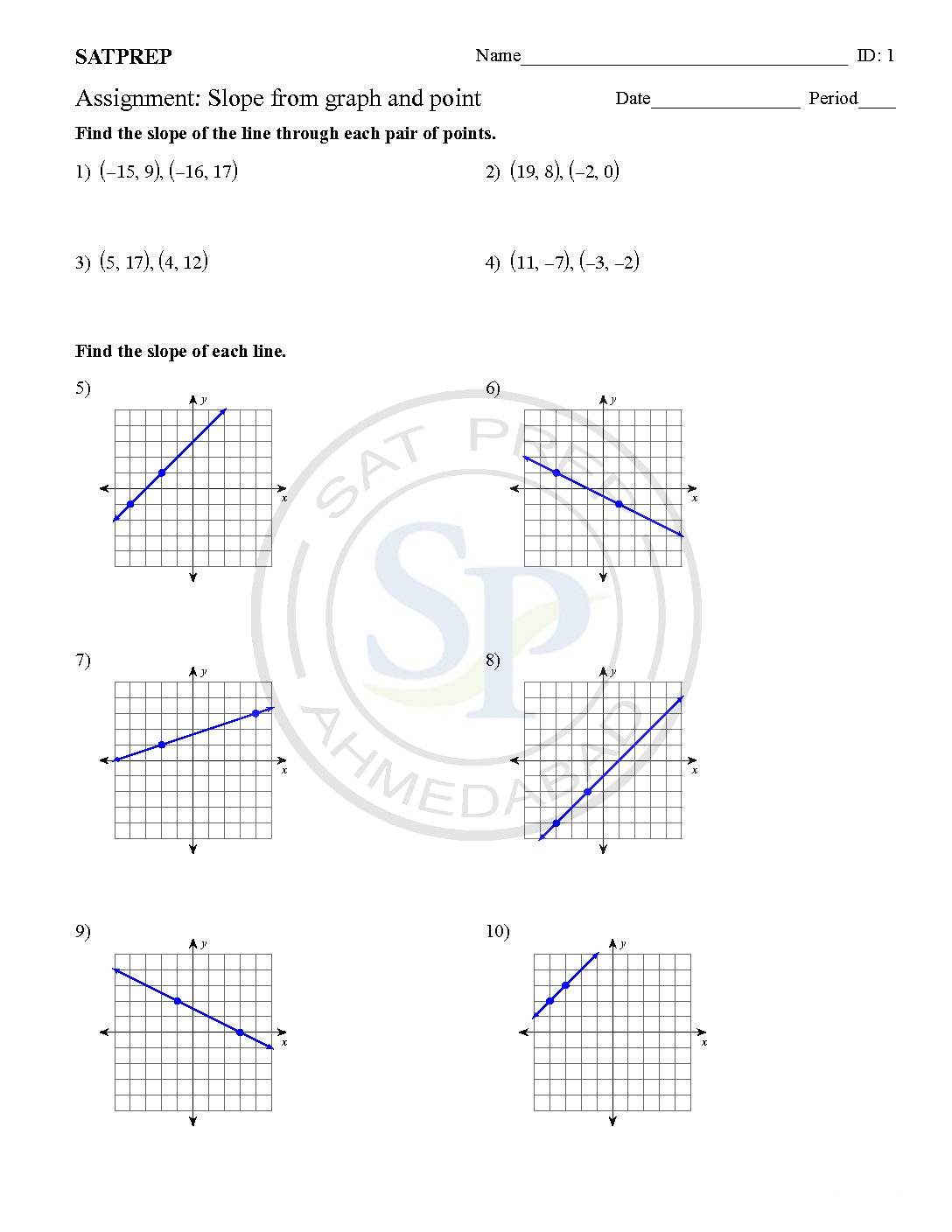
Slope from line
This post about slope of equation of lines . Eq. of line is part of coordinate geometry. coordinate geometry
Slope
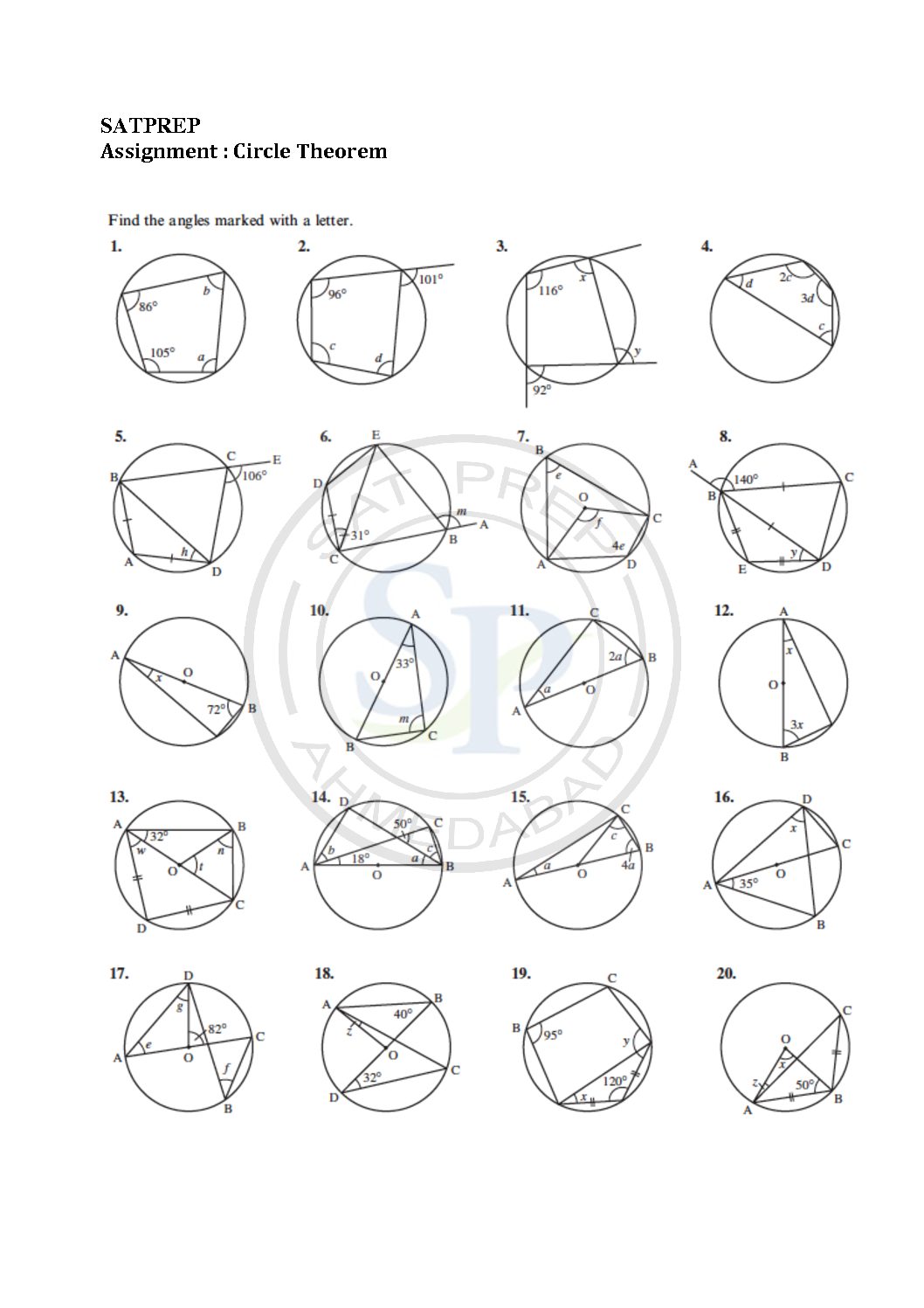
Circle Geometry
This post about is the Circle theorems. Formulas for the radius of a circle, the diameter of a circle, the circumference (perimeter) of a circle. Therefore It also include the length of chord of a circle. Because of length of chord angle also varies. Similarly other properties also involve. Explore, prove, and apply important properties of circles that have […]
St. Line Graph
Straight line graphs. The graph of each of equations is a straight line: If an equation can be rearranged into the form y = mx +c, then its graph will be a straight line. ax +by= c can be rearranged as (which can be re-written as y = mx+c). Therefore vertical lines have equations have slope undefined form x =k . Hence graph depend on […]
Radical equation
A “radical” equation is an equation in which at least one variable expression is stuck inside square root. Furthermore radical equations are one variable equation. So one root. For solving these equations , due to square root in equation , we have to square whole equation and get value of known. Radical equation
Absolute Equation
Solving absolute value equations and inequalities. And represents the distance between a and 0 on a number line. An absolute value equation is an equation that contains an absolute value expression. Has two solutions x = a and x = -a because both numbers are at the distance a from 0. Absolute Equation
Algebraic Fraction
This post about Algebraic fractions are a fraction whose numerator and denominator are algebraic expressions. Fractions in Algebra. We can add, subtract, multiply and divide fractions in algebra in the same way we do in simple arithmetic. Adding Fractions. When adding or subtracting algebraic fractions, the first thing to do is to put them onto a common denominator (by cross multiplying). Therefore we solve by […]
Imaginary No.
Complex numbers have two parts, a “real” part and an “imaginary” part (being any number with an “i” in it). The Complex numbers is ” a + bi “; that is, real-part first and part imaginary i=√(-1) due to presence to i second part is imaginary. Imaginary no
Sequence-2
Sequence and series is arrangement of term in particular pattern. Mathematical structures using the convergence properties of sequences. In particular, sequences are the basic for series Sequence and series