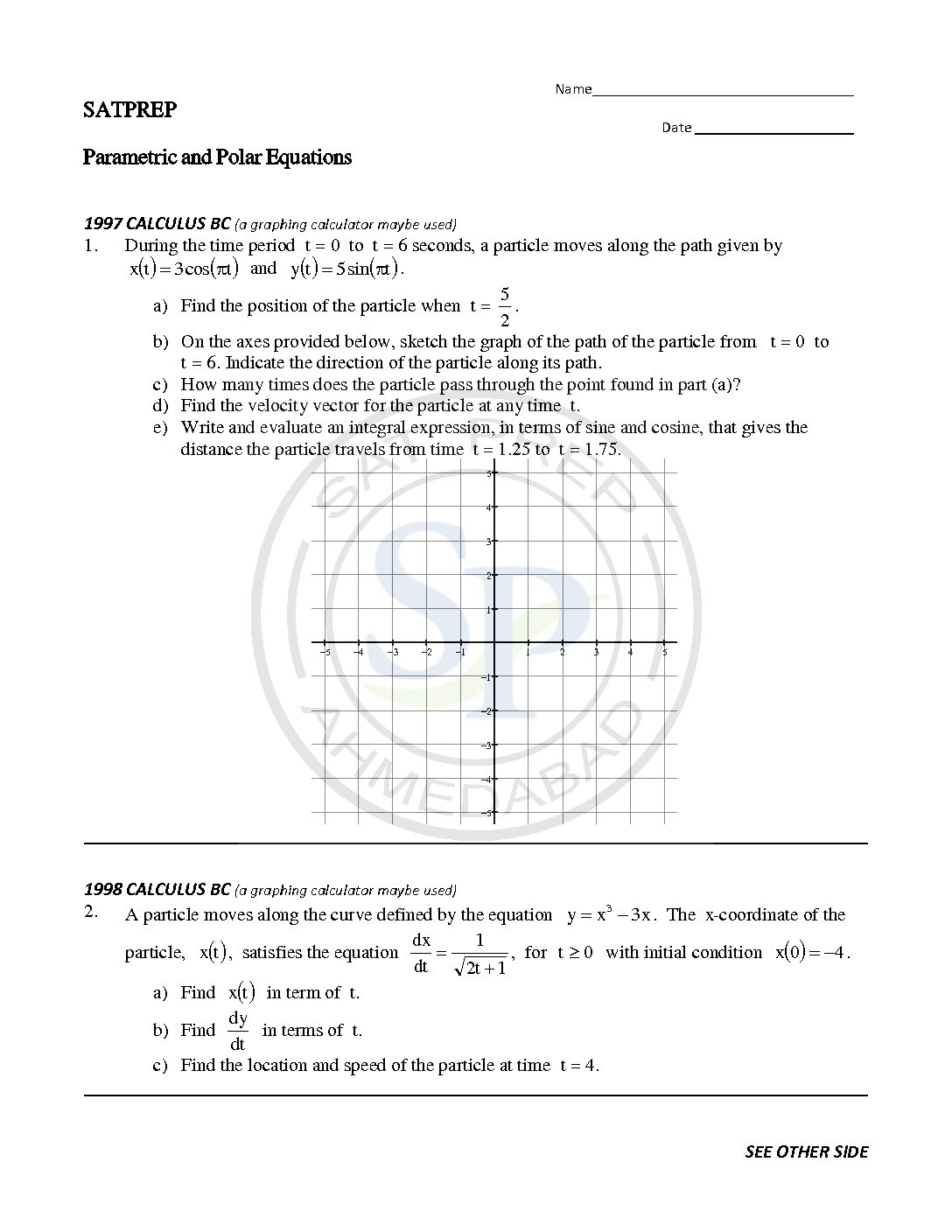
The trigonometric functions sine and cosine function. Limits and Continuity of Functions. Although we can use both radians and degrees, 𝑟𝑎𝑑𝑖𝑎𝑛𝑠radians are a more natural measurement because they are related directly to the unit circle, a circle with radius 1. trigonometric limit
You are browsing archives for
Tag: AP Calculus BC
Derivative of Parametric and Polar Equat...
This post is about derivatives of Polar and parametric Equations. Because of polar equation, Polar equation like parametric equations of the curve where the angle θ is parameter. As well as equations have parameter (r,θ). For this polar equation, the parametric equations are x ( θ) = cos θ and y ( θ) = sin θ. Therefore, the […]
Derivative of polar equation
This post is about derivatives of Polar Equations. Because of polar equation, Polar equation like parametric equations of the curve where the angle θ is parameter. As well as equations have parameter (r,θ). For this polar equation, the parametric equations are x ( θ) = cos θ and y ( θ) = sin θ. Therefore, the derivative is which […]
Derivative of Polar Equation
This post is about derivatives of Polar Equations. Because of polar equation, Polar equation like parametric equations of the curve where the angle θ is parameter. As well as equations have parameter (r,θ). For this polar equation, the parametric equations are x ( θ) = cos θ and y ( θ) = sin θ. Therefore, the derivative is which […]
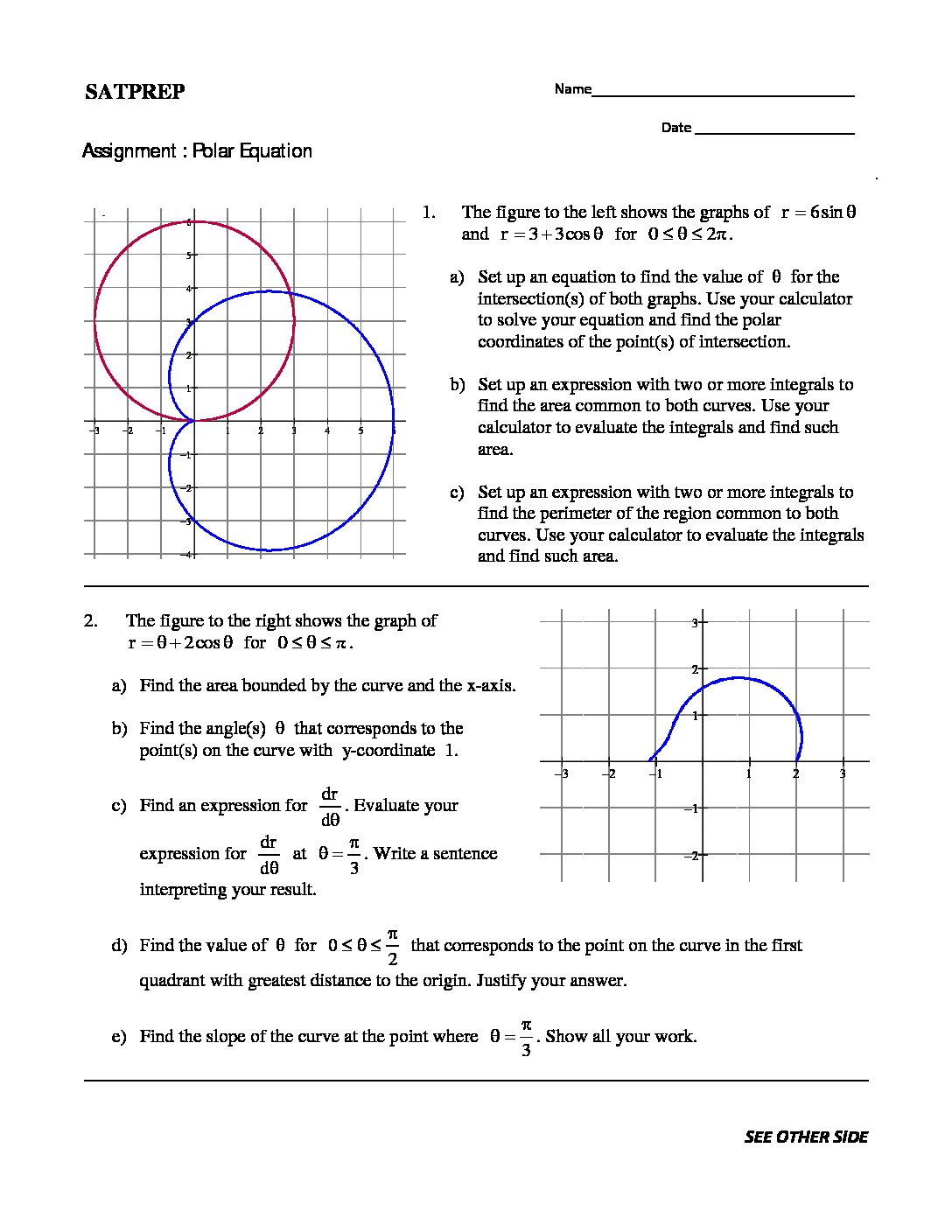
Parametric and Polar Equation
Parametric and Polar Equations , a function with two variables, x and y. In some cases, though it is useful to introduce a third variable, called a parameter, and express x and y in terms of the parameter. Polar equations ,work. Coordinates in polar equations are of the form (r,θ), where r represents radius and θ represents angle. Hence both are same type […]