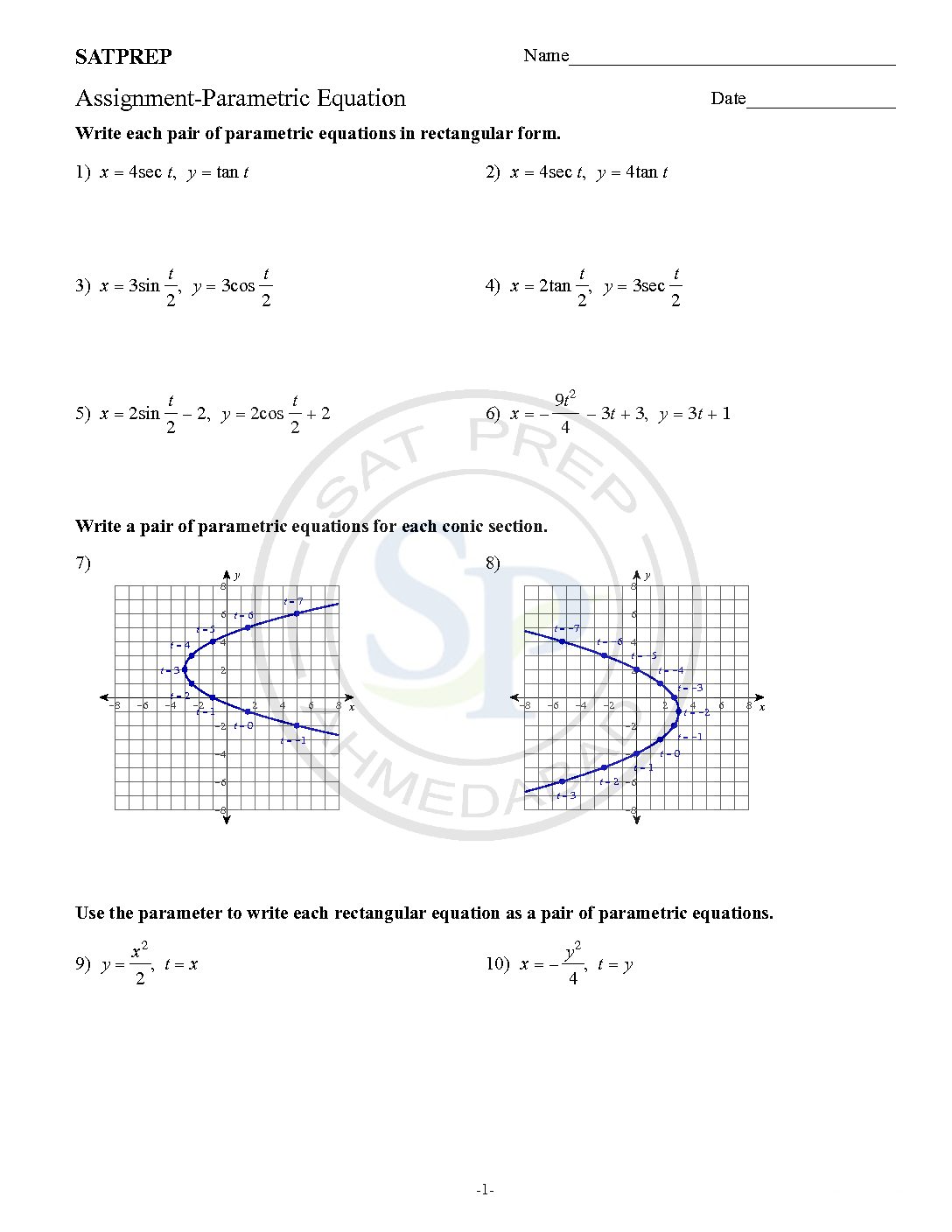
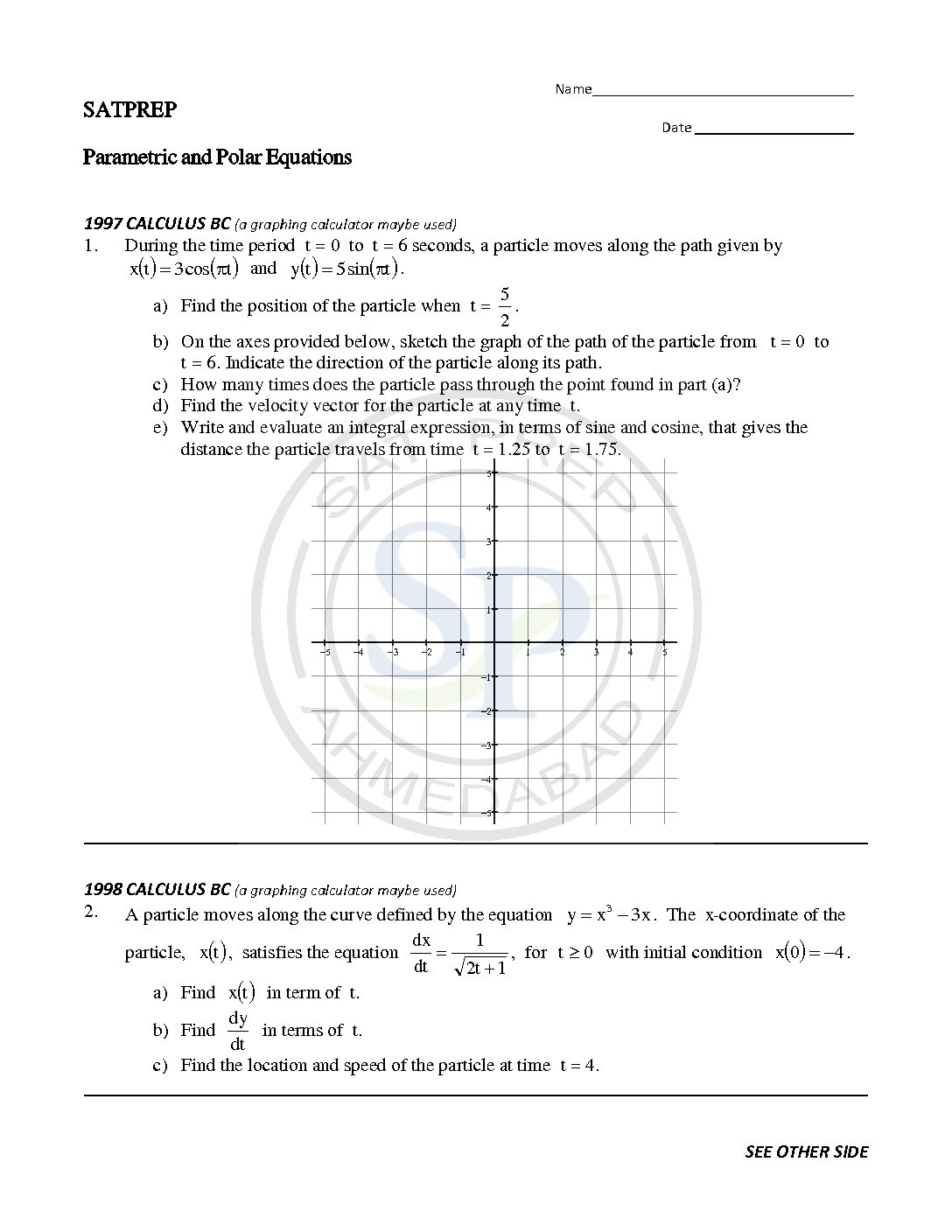
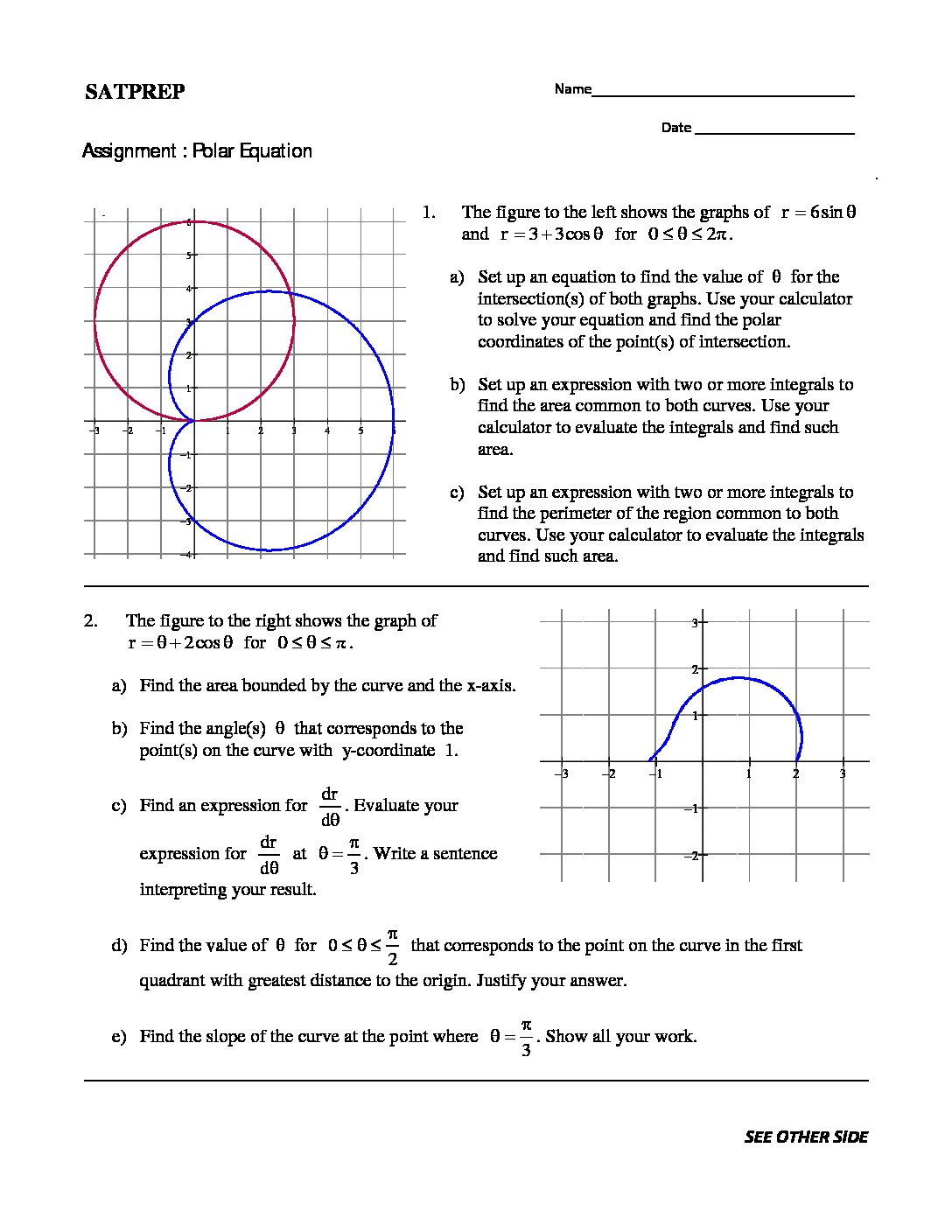
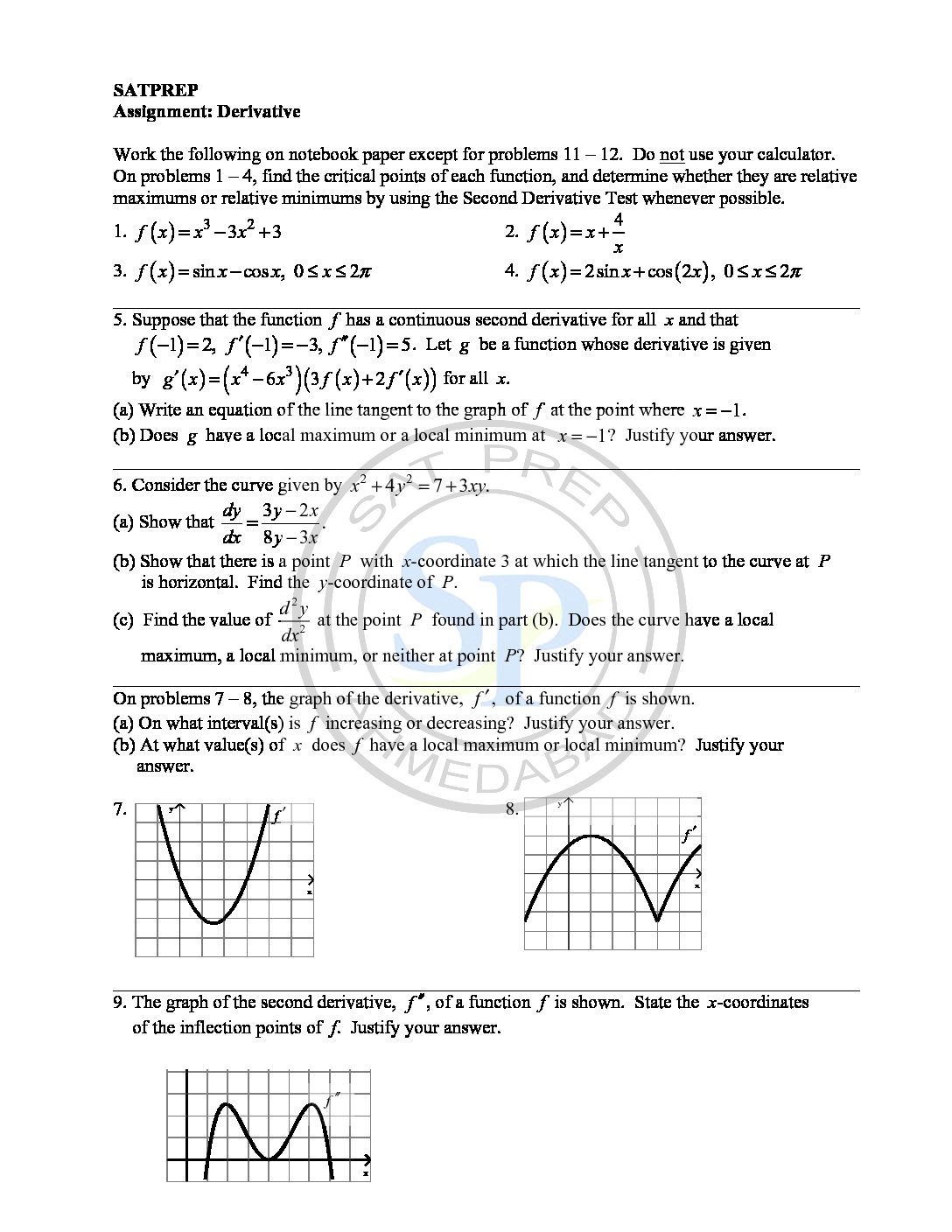
Parametric equations are three variable equation. In this type of equation two variable defines in terms of third variable to form two equation. Third common variable is know as parameter. Due to parameter these equation call parametric equation. Likewise x = f(t) and y = g(t), where t is parameter. Also we can say x […]
You are browsing archives for
Tag: Derivative
Derivative curve sketching
This post about tips to sketch derivative curve from curve . Therefore, we have to analyse curve like their intercepts , stationary point slope . derivative curve
Derivative of Parametric and Polar Equat...
This post is about derivatives of Polar and parametric Equations. Because of polar equation, Polar equation like parametric equations of the curve where the angle θ is parameter. As well as equations have parameter (r,θ). For this polar equation, the parametric equations are x ( θ) = cos θ and y ( θ) = sin θ. Therefore, the […]
Derivative of polar equation
This post is about derivatives of Polar Equations. Because of polar equation, Polar equation like parametric equations of the curve where the angle θ is parameter. As well as equations have parameter (r,θ). For this polar equation, the parametric equations are x ( θ) = cos θ and y ( θ) = sin θ. Therefore, the derivative is which […]
Kinematics
Kinematic is the branch of classical mechanics. describes the motion of points, objects and systems of groups of objects, without reference to the causes of motion. The symbol a stands for the acceleration of the object. And the symbol v stands for the instantaneous velocity of the object. The derivative of displacement with time is velocity […]
Equation of Tangent and Normal
Tangents to a curve are a line that touches the curve at one point and has the same slope as the curve at that point. A normal to a curve is a line perpendicular to a tangent to the curve. Tangent and Normal
Derivative of implicit and inverse trigo...
In calculus, a methods of implicit differentiation, Makes use of the chain rule to differentiate implicitly defined functions. To differentiate an implicit function y ( x ), defined by an equation R ( x, y) = 0, it is not generally possible to solve it explicitly for y and then differentiate. The derivatives of inverse trig functions we’ll need the formula from the last section […]
Derivative
The derivative of a function of a single variable at a chosen input value. Derivative is the slope of the tangent line to the graph of the function at that point. Hence derivative of a function y = f(x) of a variable x is a measure of the rate at which the value y of the function changes with respect to the change […]
Derivative of polynomials
Derivative is product of differentiation. Differentiation has applications to nearly all quantitative disciplines. For example, in physics, the derivative of the displacement of a moving body with respect to time is the velocity of the body, and the derivative of velocity with respect to time is acceleration. Therefore differentiation is process Derivative
Differentiation of function
The Differentiation means change in one quantity with respect to change in other. It also give of derivative of function . It also gives gradient of tangent of curve at a point. For differentiation use Power rule. Another differentiation is process for finding rate of change quantity. Rule of differentiation