Volume of revolution. To get a solid of revolution we start out with a function, y=f (x), on an interval [a,b]. We then rotate this curve about a given axis to get the surface of the solid of revolution. For purposes of this discussion let’s rotate the curve about the x -axis, although it could be any vertical […]
You are browsing archives for
Tag: Volume
Volume of revolution of solid
Volume with Rings. To get a solid of revolution we start out with a function, y=f (x), on an interval [a,b]. We then rotate this curve about a given axis to get the surface of the solid of revolution. For purposes of this discussion let’s rotate the curve about the x -axis, although it could be any vertical or […]
Volume of revolution
To get a solid of revolution we start out with a function, y=f (x), on an interval [a,b]. We then rotate this curve about a given axis to get the surface of the solid of revolution Volume of Revolution
Volume
To get a solid of revolution we start out with a function, y=f (x), on an interval [a,b]. We then rotate this curve about a given axis to get the surface of the solid of revolution. volume of revolution
Volume and surface area of solid
Surface area and Volume help us measure the size of 3D objects. We’ll start with the volume and surface area of rectangular prisms. Volume and surface area
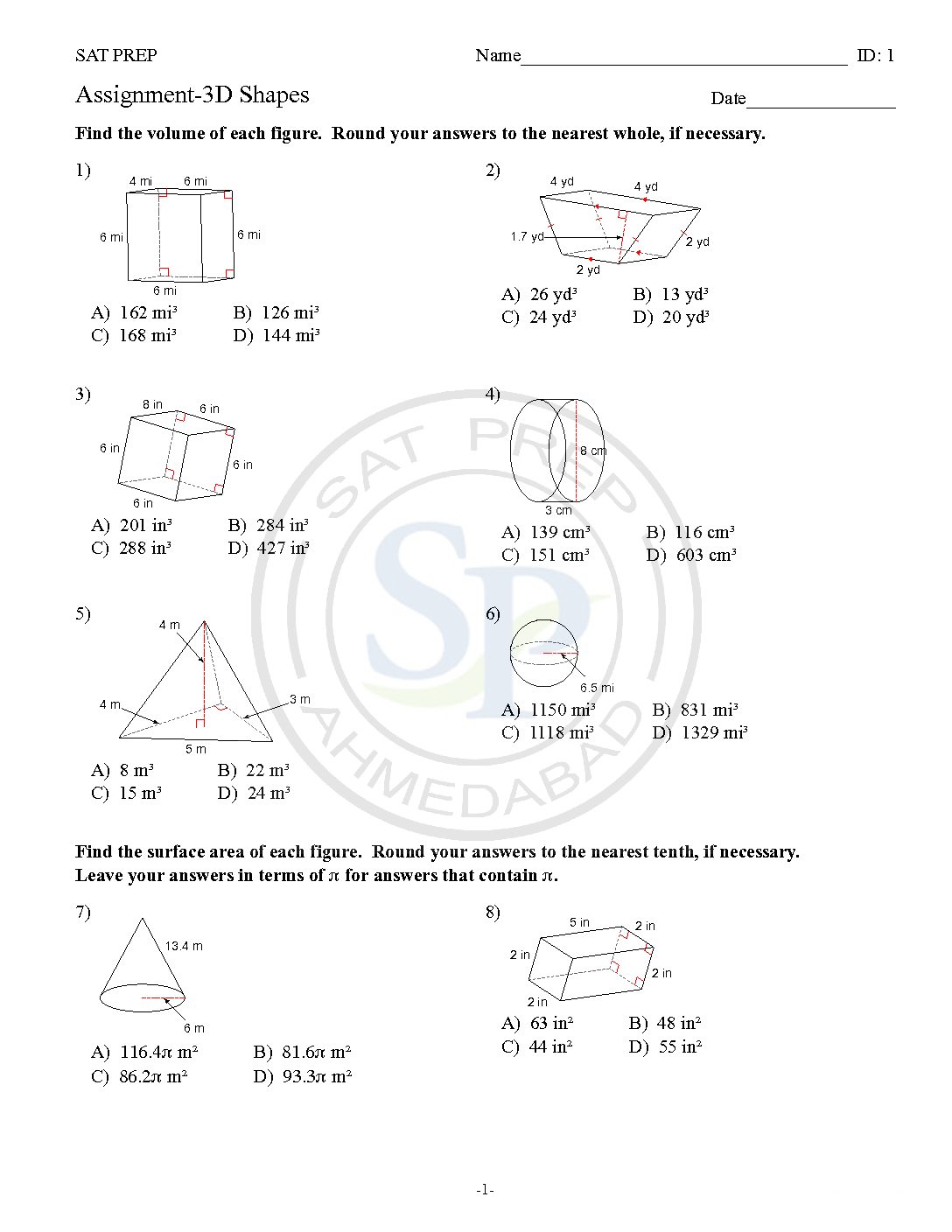
3D shapes
3D Shapes Resources. 3D shapes are solid objects that have three dimensions. These dimensions are length, width, and height. While 2D shapes are flat, 3D shapes objects that have depth to them. 3D Shapes
Integration of polynomial
Integration is way of adding functions to find the sum. Due to this concept can find areas and volumes. This also used to find equation of curve from derivative. Hence integration also called anti derivative. It is another method of Integration Numerical integration. It computing an integral with a numerical method. Integration
Volume of 3d Shapes and Sides of Polygon...
3D Shapes and Volume. 3D shapes have volume: the amount of cubic space inside of them. To find volume, you basically need the three dimensions: length, width, and height. For prisms, the formulas are derived by taking the area of the shape at the end, and multiplying that times the figure’s height. All regular polygons have at least one axial symmetry. A regular polygon with as many axes of symmetry as it possesses sides. The axes of […]