Trigonometric Equations involve one or more trigonometric ratios of unknown angles. Due to difference unit of angle , hence it gives angle in two different form. Similarly it give value in degree. Trigonometric Equation
You are browsing archives for
Category: Integration
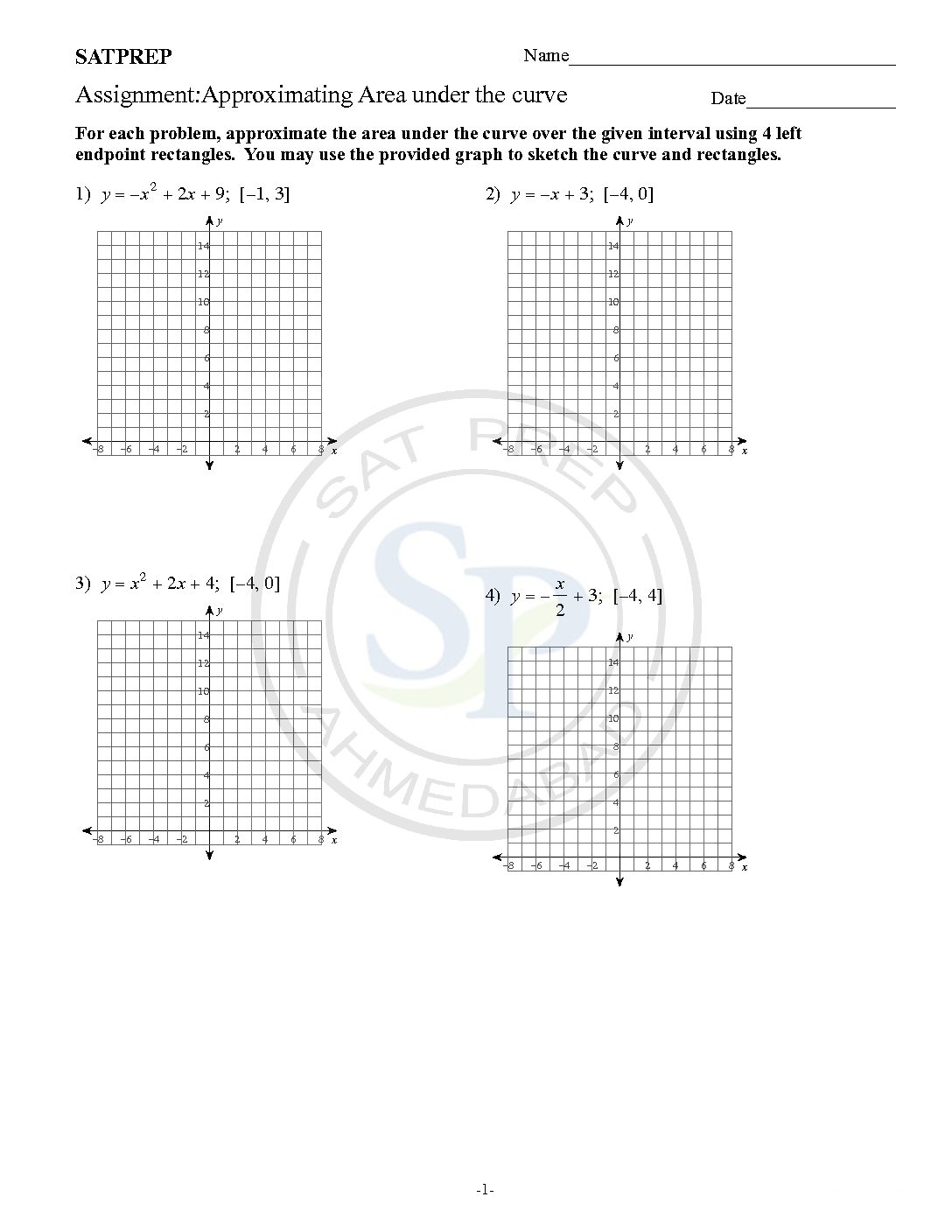
Approximating area under the curve
Approximate area of under a curve. Compute left, right, and midpoint Hence Riemann sums use with n rectangles are computed. Due to the this it approximate area. Approximate area under
Integration by Substitution-5
This post is about worksheet of integration by substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by substitution
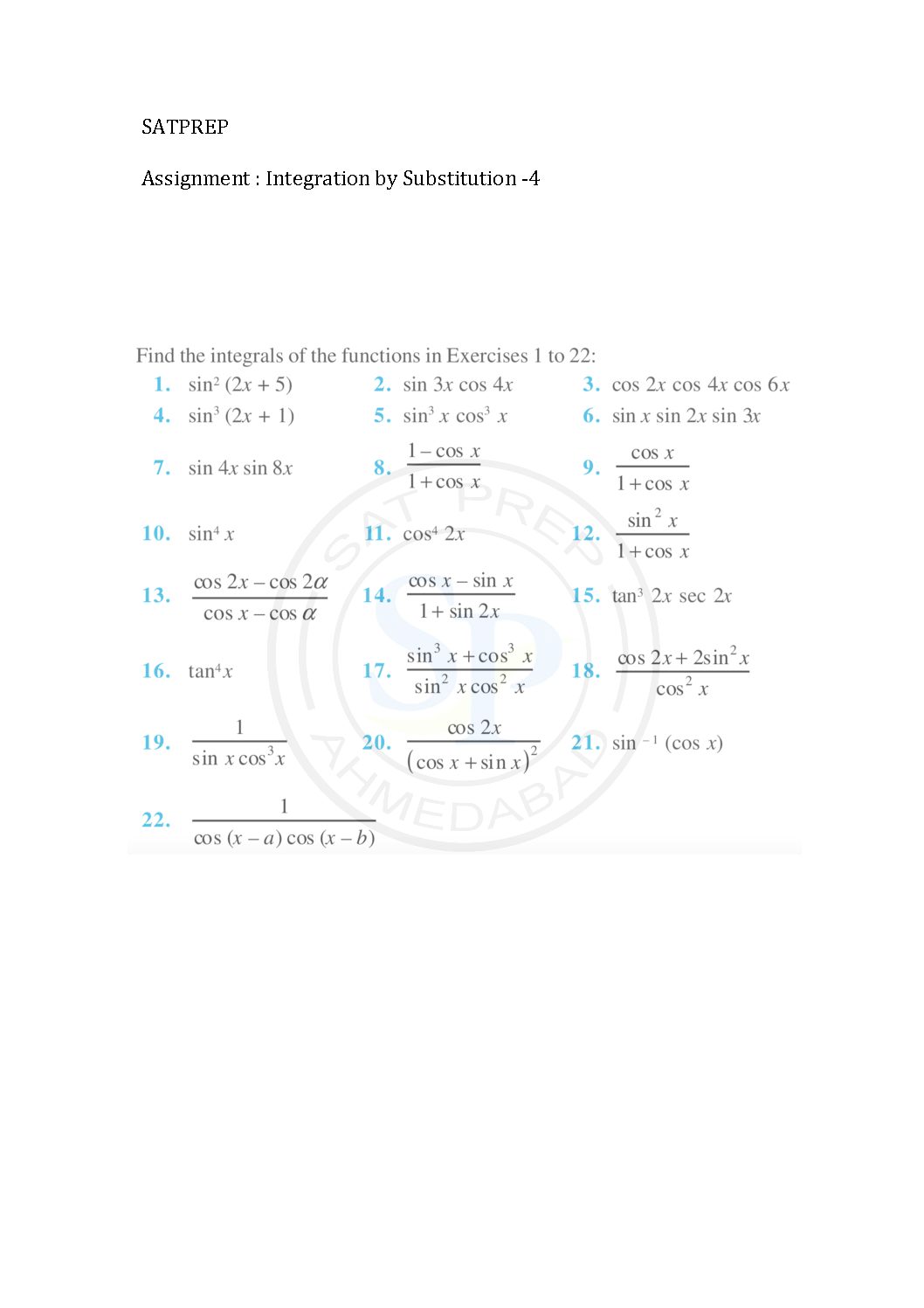
Integration by Substitution-4
This post is about worksheet of integration by substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] integration by substitution
integration by algebraic substitutions
This post is about worksheet of integration by algebraic substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by substitution
Integration of Trigonometric Function
This post is about worksheet of Integration of trigonometric functions. It also one of most important concept of integral calculus . The function ƒ(φ(t)) is also integrable on [a,b] Integration of trigonometric function
Integration of Radicals
This post about integration of polynomial with fractional power. First of all simplify expression also surds and then apply integration rule. Due to presence of constant it will give general solution. Integration
Integration of Polynomials
In integration the power of polynomials increase like quadratic become cubic etc. As well as get integration constant . It always give general solution due to integration constant. Integration
Integration by substitution -1
This post is about worksheet of Integration by exponential substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by exponential substitution
Integration by substitution -2
This post is about worksheet of integration by logarithmic substitution. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by logarithmic substitutions