First of all differentiation and Integration are process of calculus. Due to differentiation we get derivative, while integration of derivative we get function back. Integration also called derivative. Differentiation and Integration
You are browsing archives for
Category: Definite Integration
Multiple angle identity
Multiple angles identity are nothing but the trigonometric identity of multiple angles. Use for Proof of the double-angle and half-angle formulas. Solving Trigonometric Equations and Identities using Double–Angle and Half- Angle Formulas, examples and step by step solutions. Hence double angle formulae for sin 2A, cos 2A and tan 2A use for solving identity. Also to solve […]
First fundamental Theorem of Calculus
Fundamental Theorem of Calculus. If we define an area function, F (x), as the area under the curve y=f (t) from t=0 to t=x, then the area function in this case is F (x)=c∗x. We would like to be able to evaluate more integrals with a process like this, The fundamental theorem of calculus tells us that if f […]
Second fundamental Theorem of Calculus
Then F ( x) is an antiderivative of f ( x )—that is, F ‘( x) = f ( x) for all x in I. That business about the interval I is to make sure we only get limits of integration that are are reasonable for your function. Some things that wouldn’t be reasonable: Choosing […]
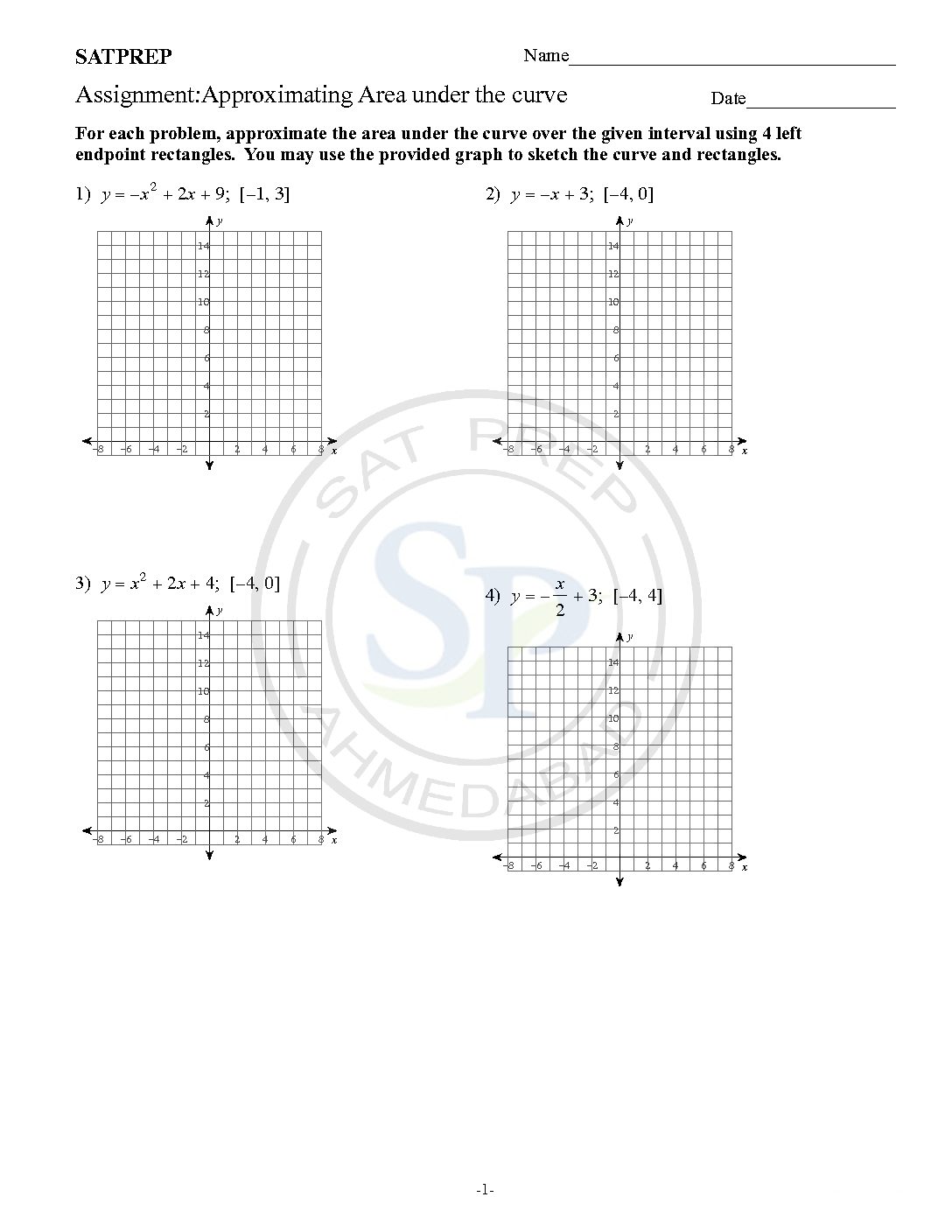
Approximating area under the curve
Approximate area of under a curve. Compute left, right, and midpoint Hence Riemann sums use with n rectangles are computed. Due to the this it approximate area. Approximate area under
integration by algebraic substitutions
This post is about worksheet of integration by algebraic substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by substitution
Integration of Trigonometric Function
This post is about worksheet of Integration of trigonometric functions. It also one of most important concept of integral calculus . The function ƒ(φ(t)) is also integrable on [a,b] Integration of trigonometric function
Riemann Sum
A Riemann sum is an approximation of a region’s area. It obtained by adding up the areas of multiple simplified slices of the region. It is applied in calculus to determine the area of a region. Hence it give approximate area of region. It is also give right and left sum. Riemann Sums
Fundamental Theorem of Calculus
FTC(Fundamental theorem calculus). If we define an area function, F (x), as the area under the curve y=f (t) from t=0 to t=x, then the area function in this case is F (x)=c∗x. We would like to be able to evaluate more integrals with a process like this, The fundamental theorem of calculus tells us that if f is […]
First fundamental theorem of calculus
First fundamental theorem of calculus If we define an area function, F (x), as the area under the curve y=f (t) from t=0 to t=x, then the area function in this case is F (x)=c∗x. The fundamental theorem of calculus shows how, in some sense, integration is the opposite of differentiation Theorem of Calculus of integration