This post about integration of polynomial with fractional power. First of all simplify expression also surds and then apply integration rule. Due to presence of constant it will give general solution. Integration
You are browsing archives for
Category: Integration
Integration of Polynomials
In integration the power of polynomials increase like quadratic become cubic etc. As well as get integration constant . It always give general solution due to integration constant. Integration
Riemann Sum
A Riemann sum is an approximation of a region’s area. It obtained by adding up the areas of multiple simplified slices of the region. It is applied in calculus to determine the area of a region. Hence it give approximate area of region. It is also give right and left sum. Riemann Sums
Fundamental Theorem of Calculus
FTC(Fundamental theorem calculus). If we define an area function, F (x), as the area under the curve y=f (t) from t=0 to t=x, then the area function in this case is F (x)=c∗x. We would like to be able to evaluate more integrals with a process like this, The fundamental theorem of calculus tells us that if f is […]
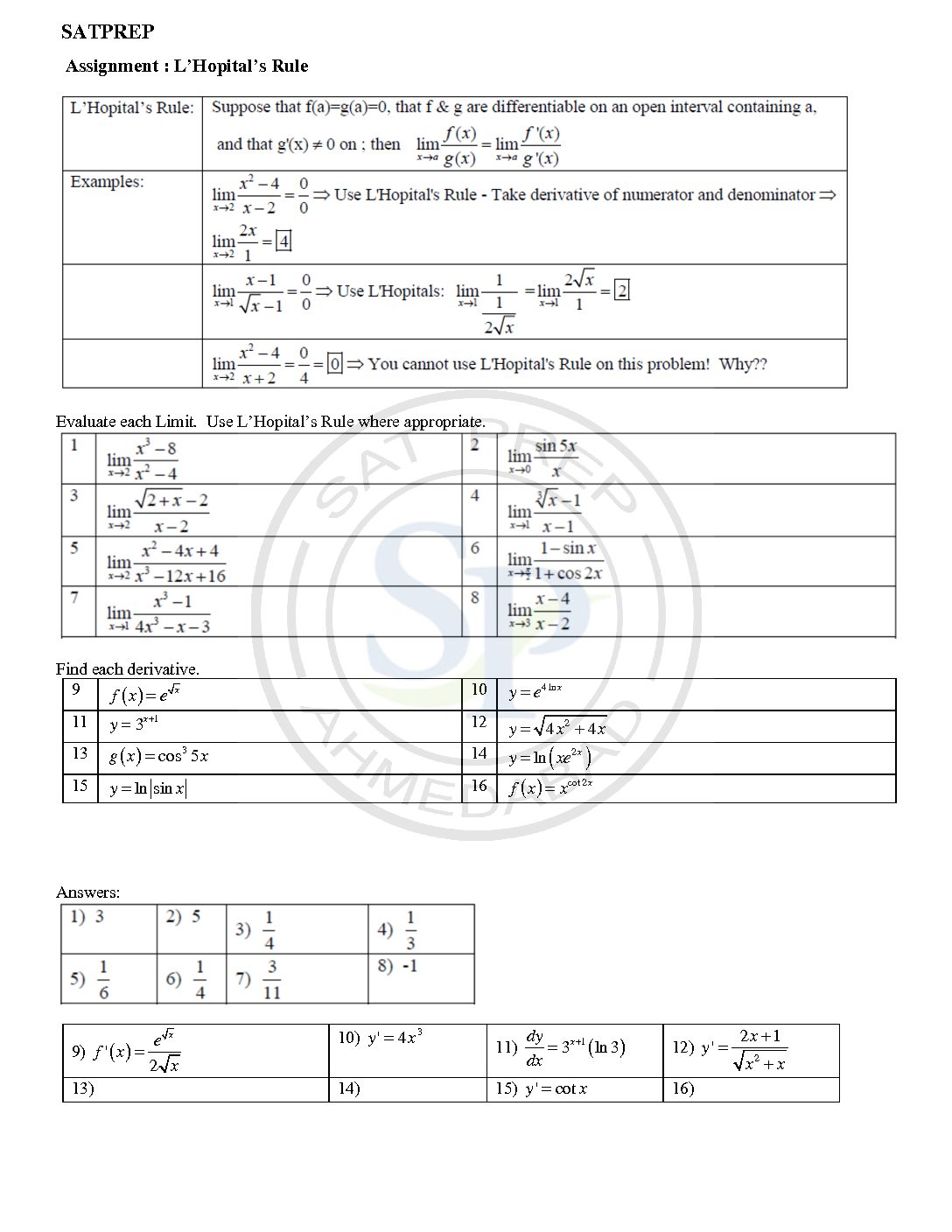
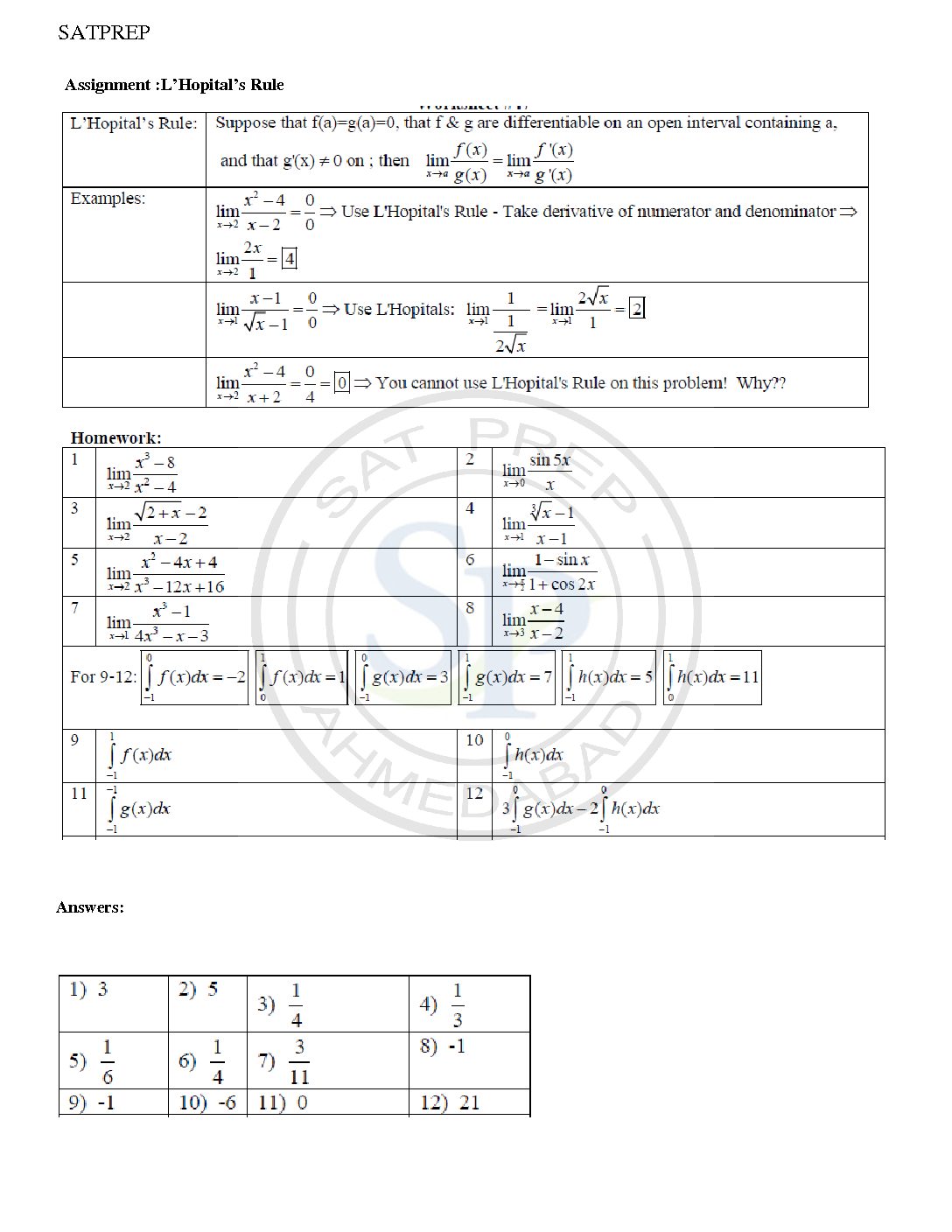
L’ Hopital Rule
L’Hospital rule is simplify evaluation of limits. It does not directly evaluate limits. Therefore L’Hospital’s Rule tells us that if we have an indeterminate form 0/0 or ∞/∞ Also it solve by differentiation. L’ Hopital’ Rule
L Hopital
L’Hospital rule is simplify evaluation of limits. It does not directly evaluate limits. Therefore L’Hospital’s Rule tells us that if we have an indeterminate form 0/0 or ∞/∞ Also it solve by differentiation. Hence it is differentiate till indeterminate form. L Hotipal
Differential Equation
A Differential Equation is a function and one or more of its derivatives. Hence it solve by variable seperable and linear differential eq method. Also it solve by homogeneous. Differential Eq
Integration by substitution -1
This post is about worksheet of Integration by exponential substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by exponential substitution
Integration by substitution -2
This post is about worksheet of integration by logarithmic substitution. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by logarithmic substitutions
Integration by Parts
By parts apply for integration when different functions are in product form . As well as one derivative of another. By parts