Sequence and series is arrangement of term in particular pattern. Mathematical structures using the convergence properties of sequences. In particular, sequences are the basic for series Sequence and series
You are browsing archives for
Category: Pure Maths
This is pure maths category under cambridge as level
Volume -2
To get a solids of revolution we start out with a function, y=f (x), on an interval [a,b]. We then rotate this curve about a given axis to get the surface of the solid of revolution. Volume
Volume
To get a solid of revolution we start out with a function, y=f (x), on an interval [a,b]. We then rotate this curve about a given axis to get the surface of the solid of revolution. volume of revolution
Integration by substitution
This post is about worksheet of integration by trigonometric substitution. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by trigonometric substitutions
Factorisation
Factorisation process we applied bracket to take common term out. Also we apply difference of square of variable. Hence we reduce no of terms in expression. Therefore factorisation and expansion are reverse process. Factorisation
Simultaneous Eq.
simultaneous equations are solve by the elimination. These equations are also solve by substitution as well as graphic method. Due to variable solution give coordinate. simultaneous equation
Sequence
Arrangement of term in particular pattern is known as sequence. A series is simply adding the terms in a sequence. An arithmetic series involves adding the terms of an arithmetic sequence. Similarly when terms are in ratio and addition , sequence as well as series will be geometric. Also when ratio is less than one than geometric series will be convergent. […]
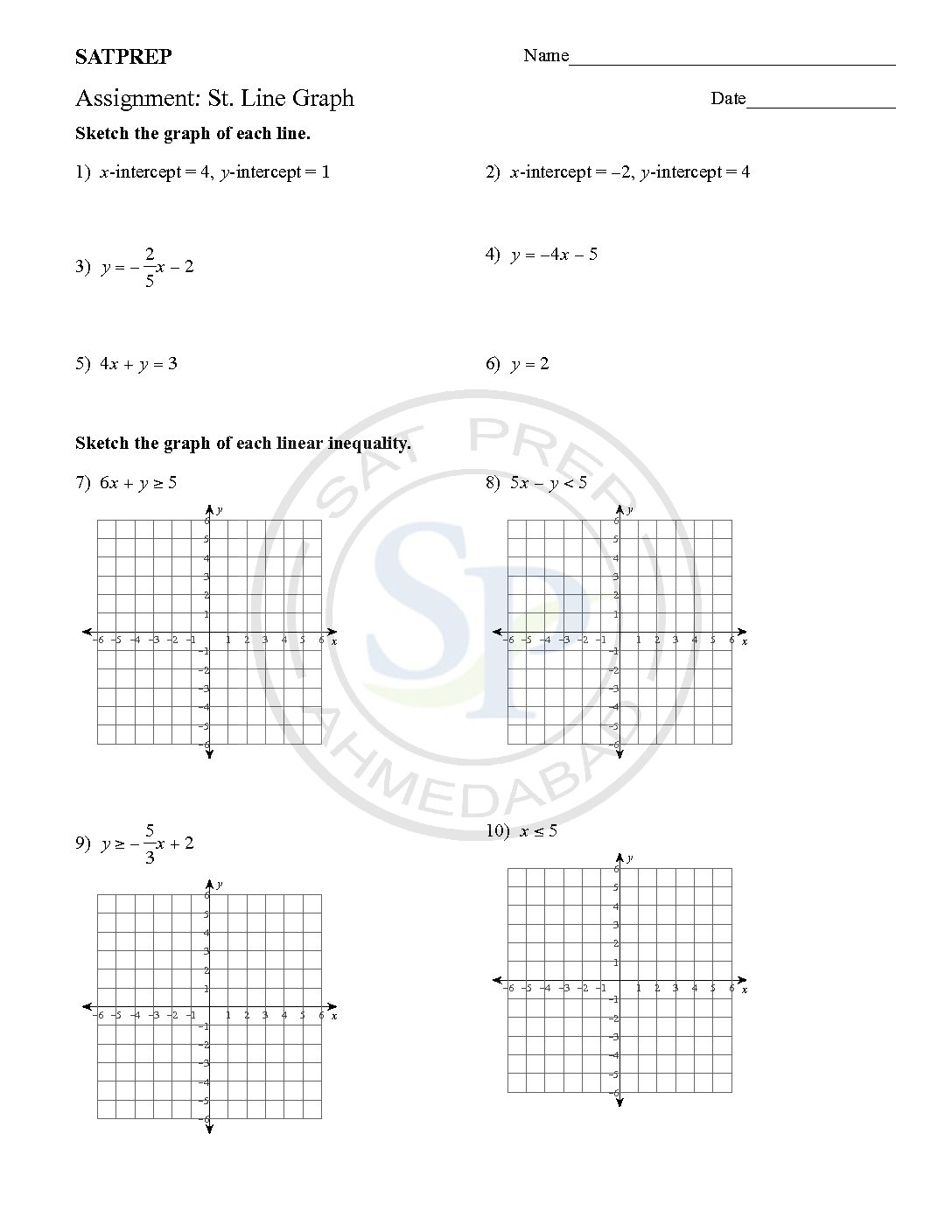
Straight line
Simultaneous Equation
The simultaneous equations are solve by the elimination. These equations are also solve by substitution as well as graphic method. Due to variable solution give coordinate. Simultaneous eq
Parabola
Vertex of a parabola is at the ‘origin’ and the axis of symmetry is along the x or y-axis, then the equation of the parabola is the simplest. So that its vertex is (h,k) and its axis of symmetry is parallel to the x-axis, it has an equation of (y – k)2= 4p (x – […]