Laws of Exponents. Exponents are also called Powers or Indices. The exponent of a number says how many times to use the number in a multiplication. Law of Indices. To manipulate expressions, we can consider using the Law of Indices. These laws only apply to expressions with the same base, for example, 3 4 and 3 2 can be manipulated […]
You are browsing archives for
Category: Cambridge Maths AS
Quadratics
First of all this post consists of questions of factorisation of quadratics . The method use to find solutions are splitting middle term and another method is formula . We also find the nature of roots of equation. The method is use to find nature is discriminant (D= b2-4ac). Discriminant is also used in formula […]
Differentiation of polynomial
Differentiation is process of getting derivative. Differentiation has applications to nearly all quantitative disciplines. For example, in physics, the derivative of the displacement of a moving body with respect to time is the velocity of the body, and the derivative of velocity with respect to time is acceleration. Similarly in chemistry as well as Economics also derivative
Formulae of Calculus
List of Calculus Formulas-basic Properties and Formulas of Integration : If f (x) and g(x) are differentiable functions . Another In basic calculus, we learn rules and formulas for differentiation, which is the method by which we calculate the derivative of a function, and integration, Differential Calculus that is concerning rates of change and slopes of curves, and Integral Calculus concerning […]
Integration by Substitution-5
This post is about worksheet of integration by substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by substitution
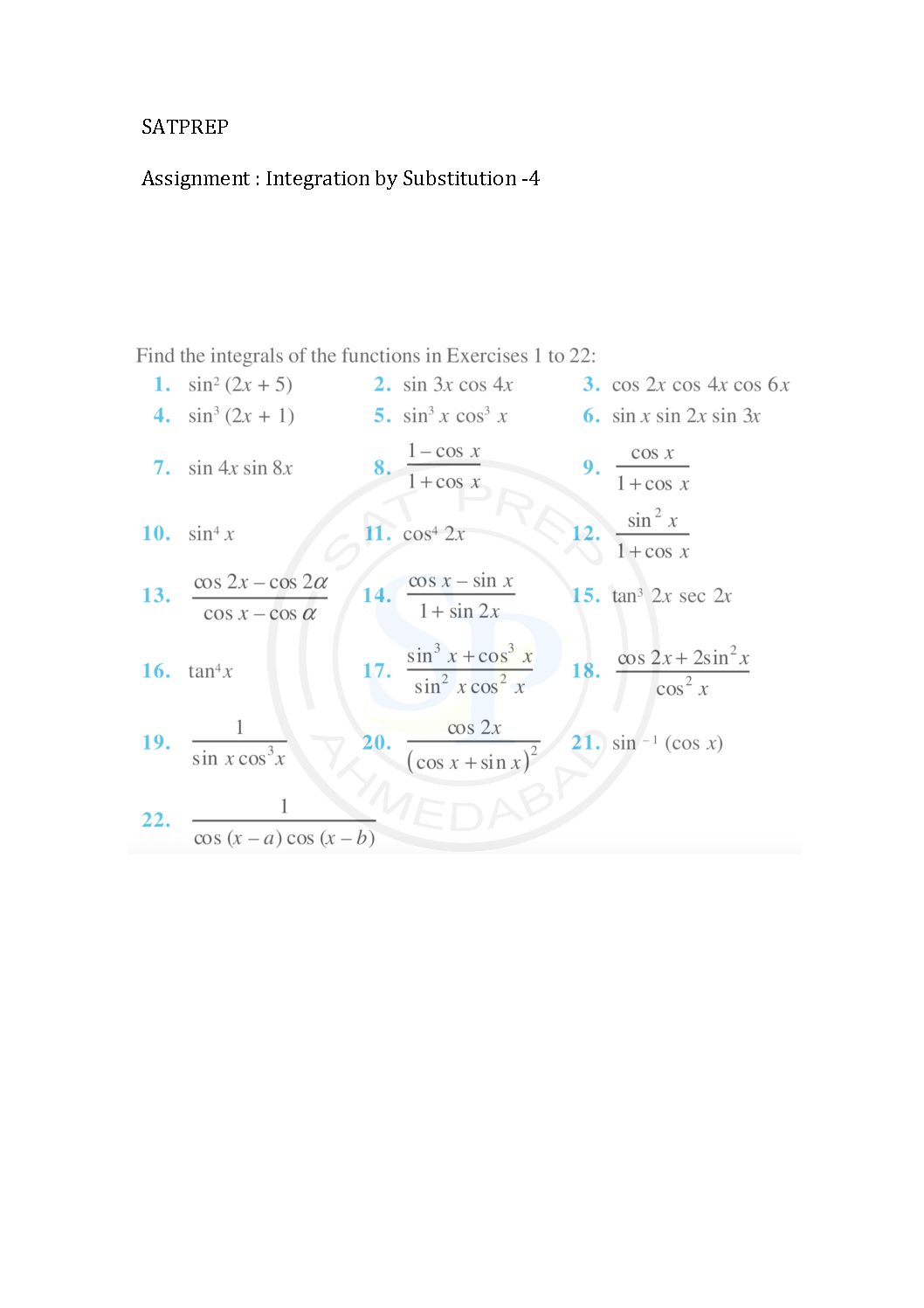
Integration by Substitution-4
This post is about worksheet of integration by substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] integration by substitution
Trigonometric Identity
Trigonometric identities showing that the identity is always true, no matter what value of x or θ is used. Because it has to hold true for all values of x, we cannot simply substitute in a few values of x to “show” that they are equal. We have to use logical steps to show that one […]
Trigonometric Equation
Solving trigonometric equations use both the reference angles and trigonometric identities The general method of solving an equation is to convert it into the form of one ratio only. Then, using these results, hence, we can obtain solutions. Trigonometric Equation
Completing Square form
Completing form is to solve a quadratic equation by changing the form of the equation so that the left side is a perfect square trinomial. Completing the square is a technique for converting a quadratic polynomial of the form ax2 + bx + c to a(x-b)2+c. Hence this method is used to convert. Similarly it use to […]
Integration of Polynomials
In integration the power of polynomials increase like quadratic become cubic etc. As well as get integration constant . It always give general solution due to integration constant. Integration