This post is about worksheet of integration by trigonometric substitution. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by trigonometric substitutions
You are browsing archives for
Category: Calculus
Differentiation and Integration
First of all differentiation and Integration are process of calculus. Due to differentiation we get derivative, while integration of derivative we get function back. Integration also called derivative. Differentiation and Integration
Derivative of implicit and inverse trigo...
In calculus, a methods of implicit differentiation, Makes use of the chain rule to differentiate implicitly defined functions. To differentiate an implicit function y ( x ), defined by an equation R ( x, y) = 0, it is not generally possible to solve it explicitly for y and then differentiate. The derivatives of inverse trig functions we’ll need the formula from the last section […]
Tangent and normal : Implicit
Tangent and Normal Lines for implicit curves are a line that touches the implicit curve at one point and has the same slope as the curve at that point. A normal to a curve is a line perpendicular to a tangent to the curve. tangent and normal
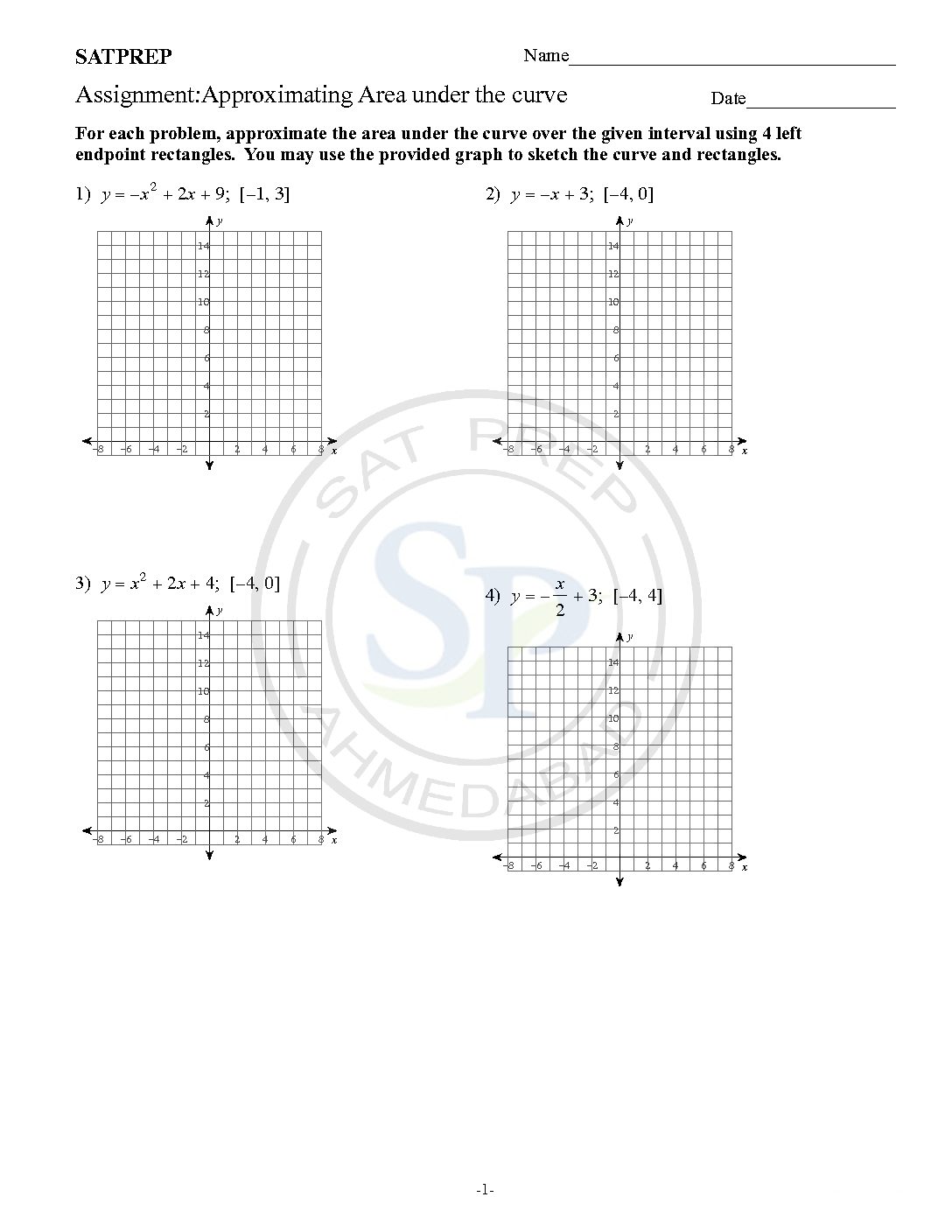
Approximating area under the curve
Approximate area of under a curve. Compute left, right, and midpoint Hence Riemann sums use with n rectangles are computed. Due to the this it approximate area. Approximate area under
Point of inflection
Inflection Point. An inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. Inflection points may be stationary points, but are not local maxima or local minima. For example, for the curve plotted above, the point is an inflection point. Point of infection
Differentiation of polynomial
Differentiation is process of getting derivative. Differentiation has applications to nearly all quantitative disciplines. For example, in physics, the derivative of the displacement of a moving body with respect to time is the velocity of the body, and the derivative of velocity with respect to time is acceleration. Similarly in chemistry as well as Economics also derivative
Formulae of Calculus
List of Calculus Formulas-basic Properties and Formulas of Integration : If f (x) and g(x) are differentiable functions . Another In basic calculus, we learn rules and formulas for differentiation, which is the method by which we calculate the derivative of a function, and integration, Differential Calculus that is concerning rates of change and slopes of curves, and Integral Calculus concerning […]
Integration by Substitution-5
This post is about worksheet of integration by substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by substitution
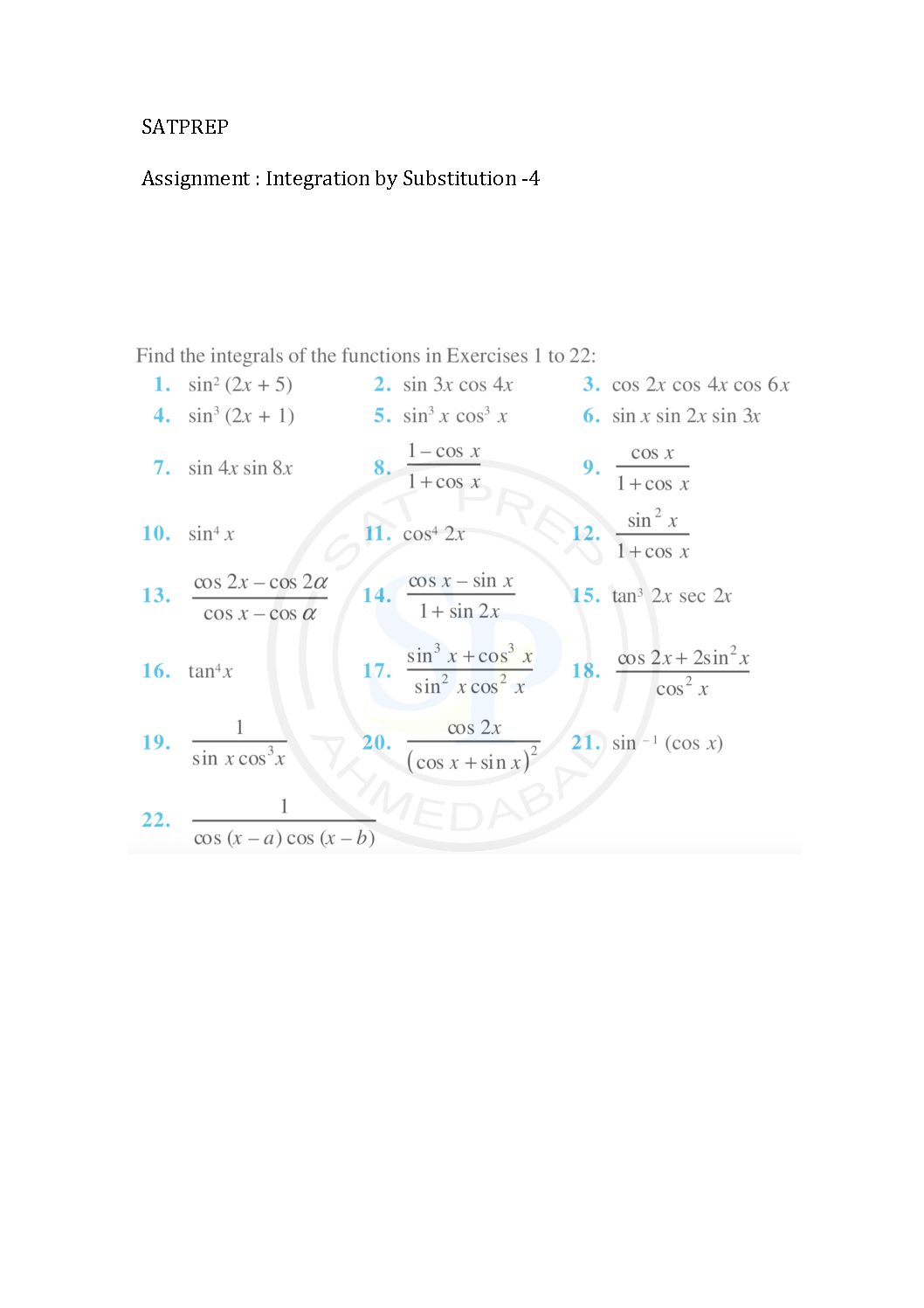
Integration by Substitution-4
This post is about worksheet of integration by substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] integration by substitution