This post about integration of polynomial with fractional power. First of all simplify expression also surds and then apply integration rule. Due to presence of constant it will give general solution. Integration
You are browsing archives for
Category: IB Maths HL
Trigonometric Identity
Trigonometric identities showing that the identity is always true, no matter what value of x or θ is used. Because it has to hold true for all values of x, we cannot simply substitute in a few values of x to “show” that they are equal. We have to use logical steps to show that one […]
Trigonometric Equation
Solving trigonometric equations use both the reference angles and trigonometric identities The general method of solving an equation is to convert it into the form of one ratio only. Then, using these results, hence, we can obtain solutions. Trigonometric Equation
Completing Square form
Completing form is to solve a quadratic equation by changing the form of the equation so that the left side is a perfect square trinomial. Completing the square is a technique for converting a quadratic polynomial of the form ax2 + bx + c to a(x-b)2+c. Hence this method is used to convert. Similarly it use to […]
Integration of Polynomials
In integration the power of polynomials increase like quadratic become cubic etc. As well as get integration constant . It always give general solution due to integration constant. Integration
Riemann Sum
A Riemann sum is an approximation of a region’s area. It obtained by adding up the areas of multiple simplified slices of the region. It is applied in calculus to determine the area of a region. Hence it give approximate area of region. It is also give right and left sum. Riemann Sums
Fundamental Theorem of Calculus
FTC(Fundamental theorem calculus). If we define an area function, F (x), as the area under the curve y=f (t) from t=0 to t=x, then the area function in this case is F (x)=c∗x. We would like to be able to evaluate more integrals with a process like this, The fundamental theorem of calculus tells us that if f is […]
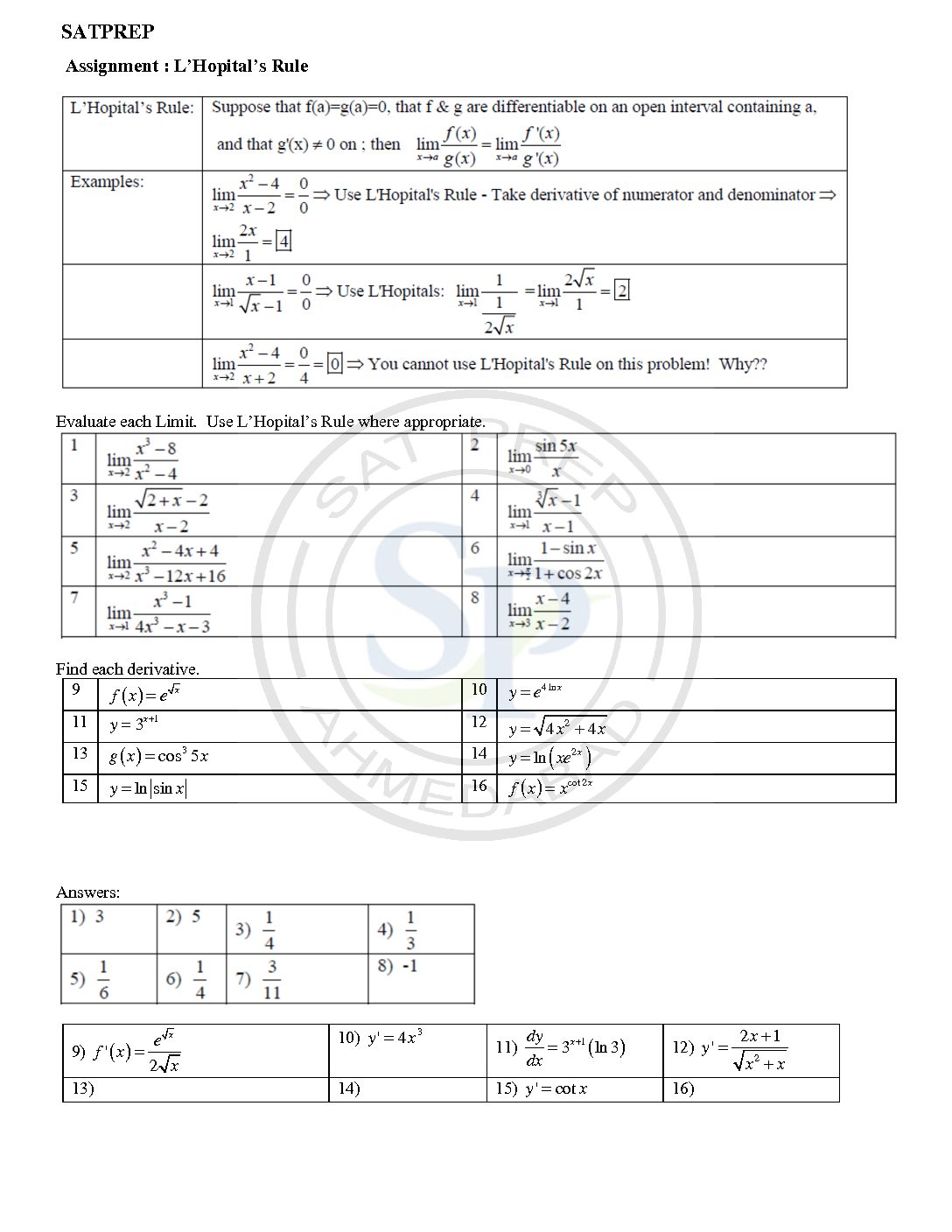
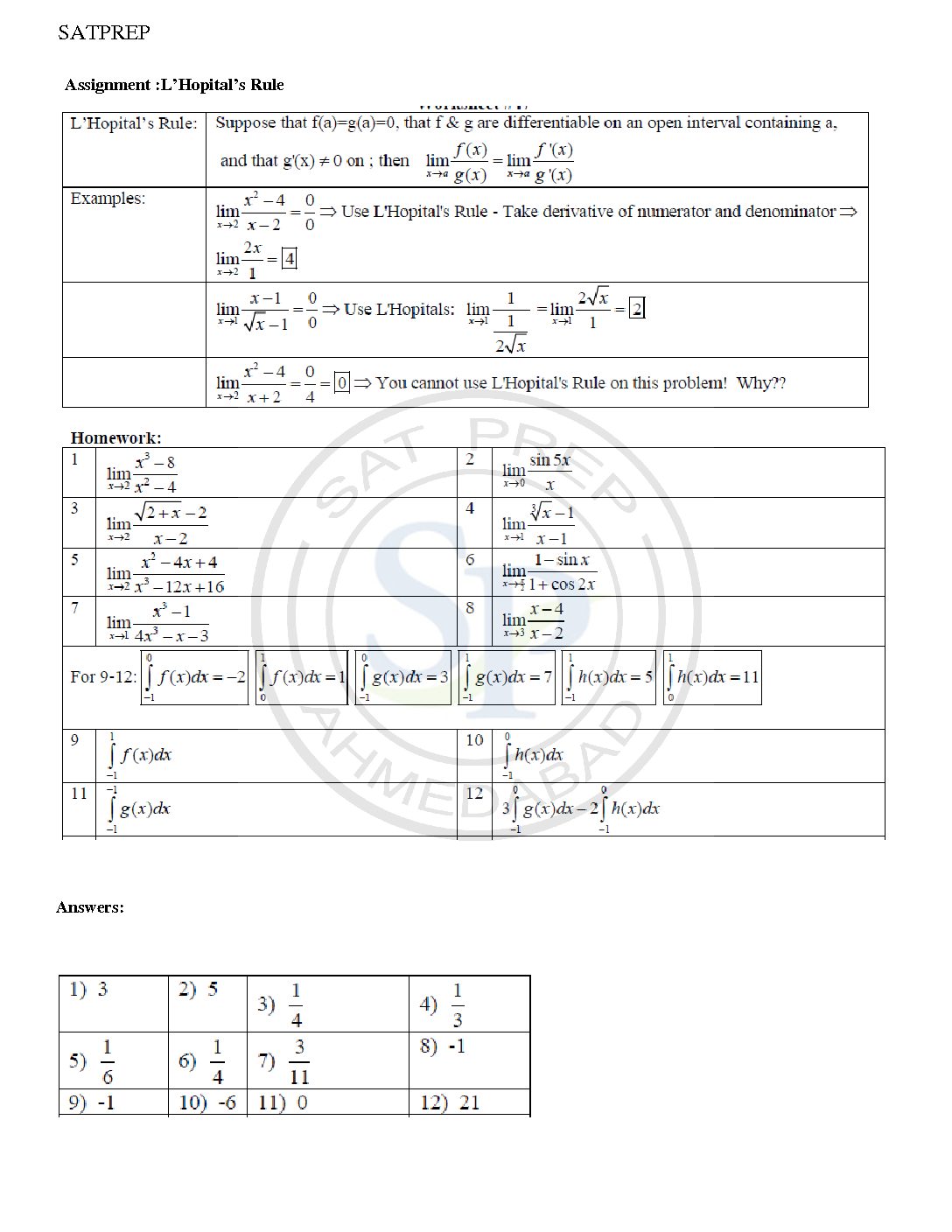
L’ Hopital Rule
L’Hospital rule is simplify evaluation of limits. It does not directly evaluate limits. Therefore L’Hospital’s Rule tells us that if we have an indeterminate form 0/0 or ∞/∞ Also it solve by differentiation. L’ Hopital’ Rule
L Hopital
L’Hospital rule is simplify evaluation of limits. It does not directly evaluate limits. Therefore L’Hospital’s Rule tells us that if we have an indeterminate form 0/0 or ∞/∞ Also it solve by differentiation. Hence it is differentiate till indeterminate form. L Hotipal
Function
A functions f(x) tells you what to do with the input, but, to be completely defined, function also need to know what type of input is permitted to go into the function. Function