This post is about worksheet of Integration by substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by substitution
You are browsing archives for
Category: IB Maths HL
Definite integration
A Definite Integral has start and end values. In other words there is an interval [a, b]. Hence , definite integral gives particular solution. Definite Integration
Maxima and minima
Maximum and Minima of Points of Inflection. The value f ‘(x) is the gradient at any point but often we want to find the Turning or Stationary Point (Maximum and Minimum points) or Point of Inflection These happen where the gradient is zero, f ‘(x) = 0. Critical Points include Turning points and Points where f ‘ (x) does not exist. […]
Equation of Tangent and Normal
A tangent to a curves are a line that touches the curve at one point and has the same slope as the curve at that point. A normal to a curve is a line perpendicular to a tangent to the curve. Tangent and normal
Rules of derivative
Rules for derivatives. Rules for derivatives. Sum rule: The derivative of the sum or difference of two functions is the sum or difference of their derivatives. (u + v)’ = u’ + v’ Constant multiple: The derivative of a constant times a function is the constant times the derivative of the function. (ku)’ = ku’ Rules for derivative
Rules of derivative
Rule for derivatives. Rules for derivatives. Sum rule: The derivative of the sum or difference of two functions is the sum or difference of their derivatives. (u + v)’ = u’ + v’ Constant multiple: The derivative of a constant times a function is the constant times the derivative of the function. (ku)’ = ku’ Rules of derivative
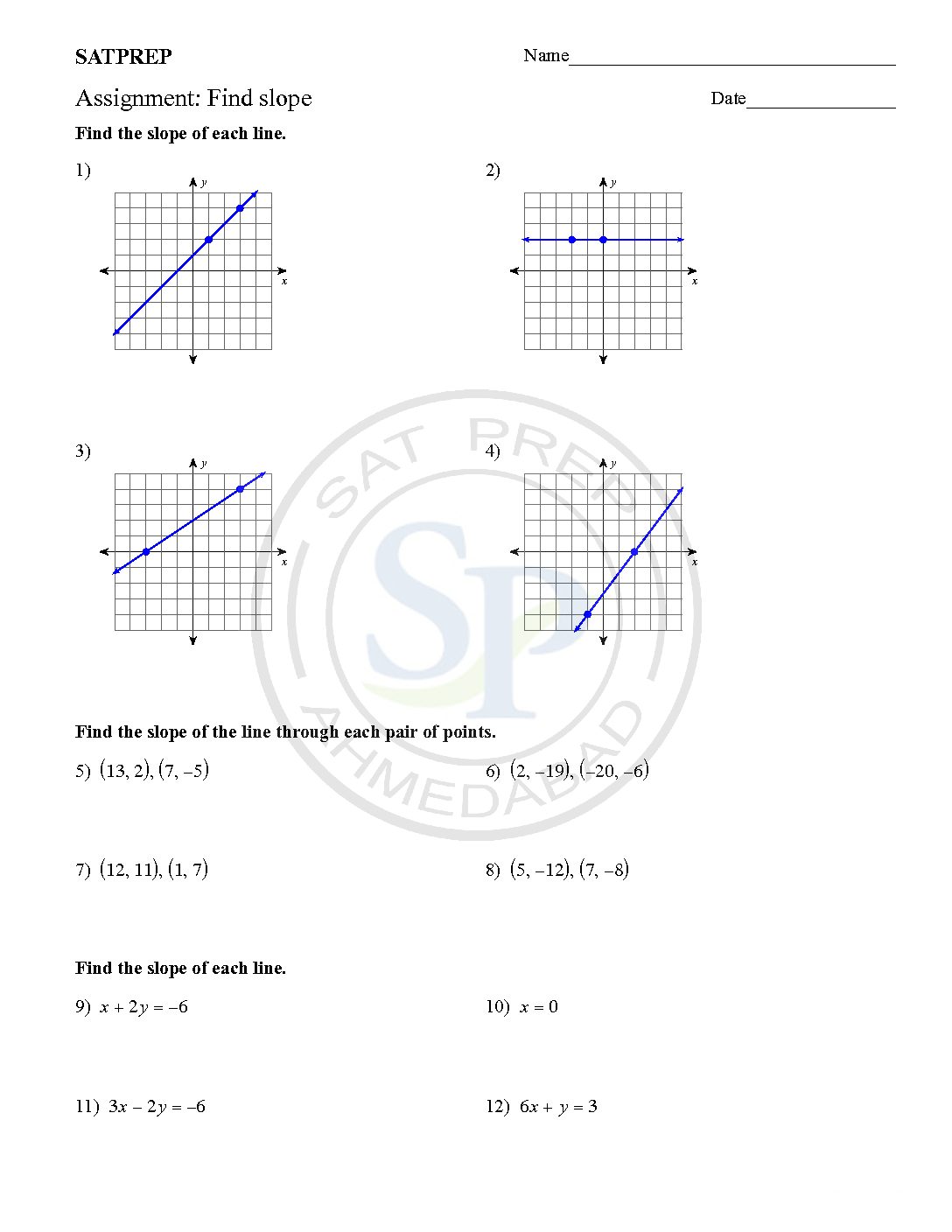
Find slope
Volume of revolution of solid
Volume of revolution. To get a solid of revolution we start out with a function, y=f (x), on an interval [a,b]. We then rotate this curve about a given axis to get the surface of the solid of revolution. For purposes of this discussion let’s rotate the curve about the x -axis, although it could be any vertical […]
Volume of revolution of solid
Volume with Rings. To get a solid of revolution we start out with a function, y=f (x), on an interval [a,b]. We then rotate this curve about a given axis to get the surface of the solid of revolution. For purposes of this discussion let’s rotate the curve about the x -axis, although it could be any vertical or […]
St. Line Graph
Straight line graphs. The graph of each of equations is a straight line: If an equation can be rearranged into the form y = mx +c, then its graph will be a straight line. ax +by= c can be rearranged as (which can be re-written as y = mx+c). Therefore vertical lines have equations have slope undefined form x =k . Hence graph depend on […]