You are browsing archives for
Category: Calculus
Topic wise solutions to IBDP Math SL Pap...
This post is about the solution of questions of calculus from Math SL Paper -2 . In this post questions are from Nov 2011 to Nov 2019. By this post students will come to know variety of questions asked in previous year papers. The questions type in this post is calculator . www.ibo.org
Topic wise IBDP Math SL Paper 2 Calculus
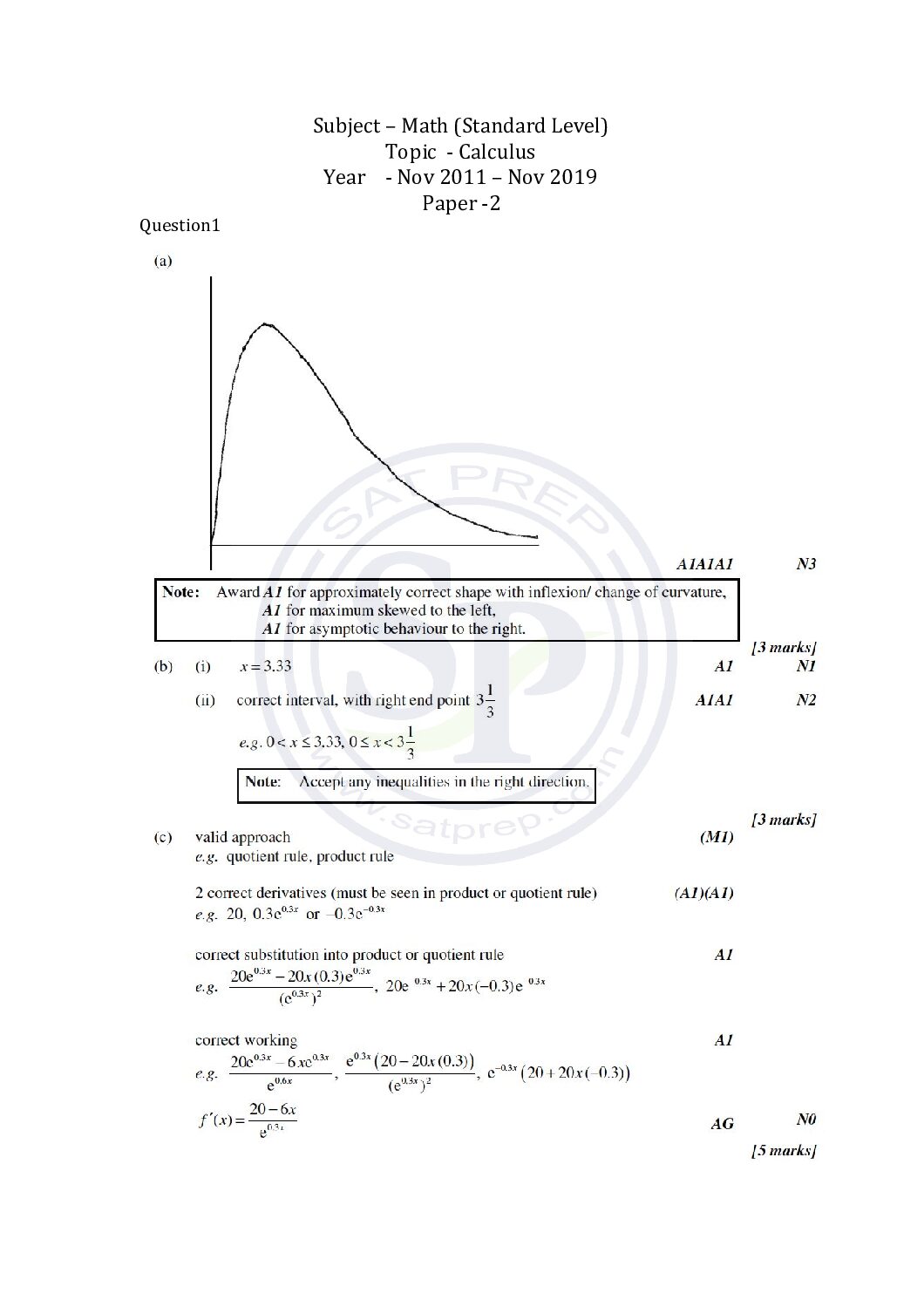
This post is about the question of calculus Math SL Paper -2 past paper. In this post questions are from different paper from Nov 2011 to Nov 2019. By this post students will come to know variety of questions asked in previous year papers. The questions type in this post is calculator . www.ibo.org […]
Topic wise IBDP Math SL Paper 1 Calculus
Calculus questions of IBDP Math SL Paper 1 from past papers. This post is about Calculus questions of Non Calculator past papers. All question from different paper from Nov 2011 to Nov 2019. By this post user will come to know verity of questions asked in past papers. Past paper
Maxima and minima
A high point of curve is called a maxima. A low point is called a minima. In the Curve only one global maxima or minima exists , while more than one local maximum or minimum. Due to curve turn on these point are called local. Hence these point also called stationary points. Maxima and minima
Integration by substitution
This post is about worksheet of Integration by substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by substitution
Definite integration
A Definite Integral has start and end values. In other words there is an interval [a, b]. Hence , definite integral gives particular solution. Definite Integration
Maxima and minima
Maximum and Minima of Points of Inflection. The value f ‘(x) is the gradient at any point but often we want to find the Turning or Stationary Point (Maximum and Minimum points) or Point of Inflection These happen where the gradient is zero, f ‘(x) = 0. Critical Points include Turning points and Points where f ‘ (x) does not exist. […]
Rules of derivative
Rules for derivatives. Rules for derivatives. Sum rule: The derivative of the sum or difference of two functions is the sum or difference of their derivatives. (u + v)’ = u’ + v’ Constant multiple: The derivative of a constant times a function is the constant times the derivative of the function. (ku)’ = ku’ Rules for derivative
Rules of derivative
Rule for derivatives. Rules for derivatives. Sum rule: The derivative of the sum or difference of two functions is the sum or difference of their derivatives. (u + v)’ = u’ + v’ Constant multiple: The derivative of a constant times a function is the constant times the derivative of the function. (ku)’ = ku’ Rules of derivative