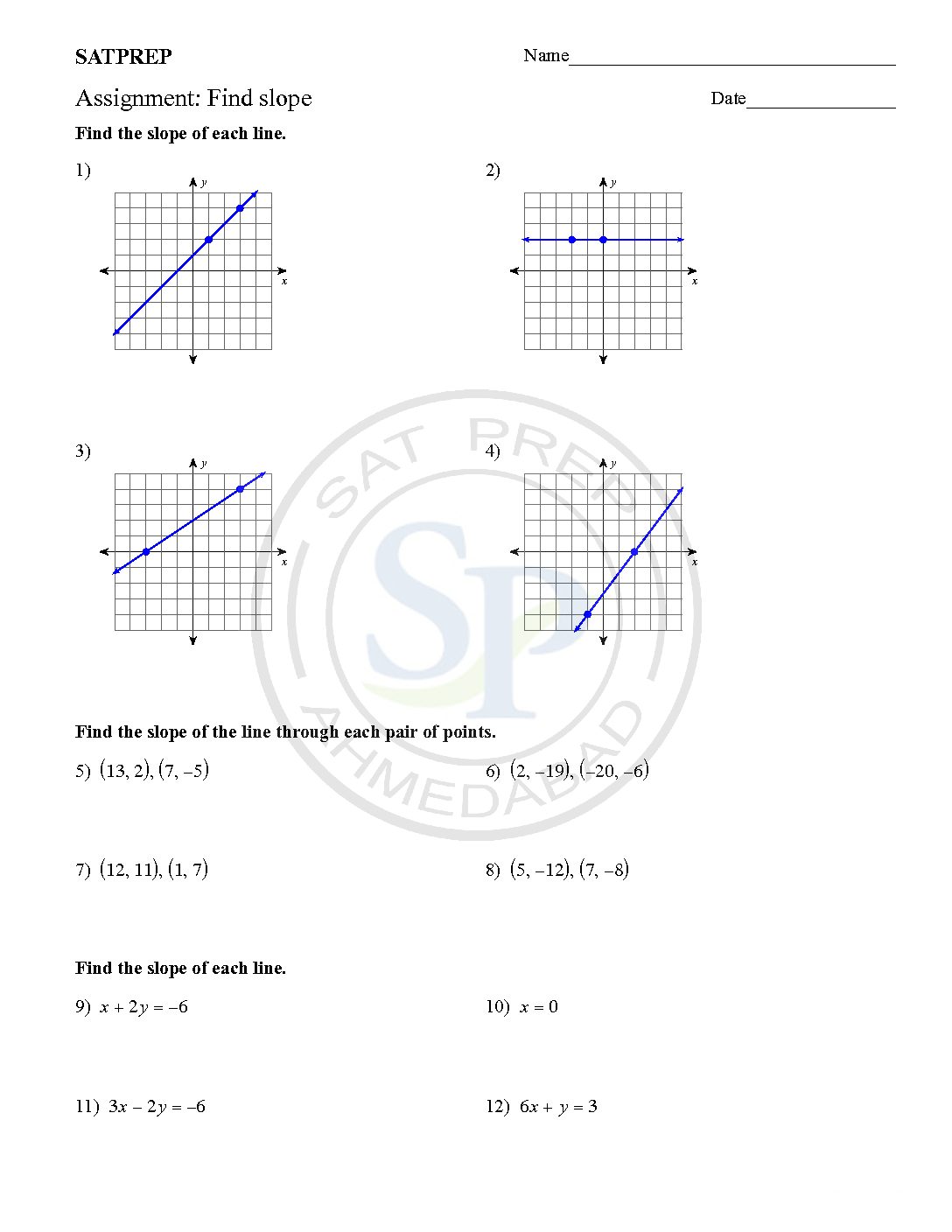
The slope of line also called gradient of line. Hence we use in equation of line. The slope
You are browsing archives for
Category: Calculus
Volume of revolution of solid
Volume of revolution. To get a solid of revolution we start out with a function, y=f (x), on an interval [a,b]. We then rotate this curve about a given axis to get the surface of the solid of revolution. For purposes of this discussion let’s rotate the curve about the x -axis, although it could be any vertical […]
Volume of revolution of solid
Volume with Rings. To get a solid of revolution we start out with a function, y=f (x), on an interval [a,b]. We then rotate this curve about a given axis to get the surface of the solid of revolution. For purposes of this discussion let’s rotate the curve about the x -axis, although it could be any vertical or […]
Kinematics
Kinematic is the branch of classical mechanics. describes the motion of points, objects and systems of groups of objects, without reference to the causes of motion. The symbol a stands for the acceleration of the object. And the symbol v stands for the instantaneous velocity of the object. The derivative of displacement with time is velocity […]
Volume of revolution
To get a solid of revolution we start out with a function, y=f (x), on an interval [a,b]. We then rotate this curve about a given axis to get the surface of the solid of revolution Volume of Revolution
Equation of Tangent and Normal
Tangents to a curve are a line that touches the curve at one point and has the same slope as the curve at that point. A normal to a curve is a line perpendicular to a tangent to the curve. Tangent and Normal
Product to Sum
Product‐Sum and Sum‐Product Identities. The process of converting products into sums can make a difference . Integrate \( \int \! \sin 3x \cos 4x \, \mathrm{d}x.\) This problem may seem tough at first, but after using the product-to-sum trigonometric formula, this integral very quickly changes into a standard form . Converting a sum of trig functions into a product. Write as and then […]
Volume
To get a solid of revolution we start out with a function, y=f (x), on an interval [a,b]. We then rotate this curve about a given axis to get the surface of the solid of revolution. volume of revolution
Integration by substitution
This post is about worksheet of integration by trigonometric substitution. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by trigonometric substitutions
Differentiation and Integration
First of all differentiation and Integration are process of calculus. Due to differentiation we get derivative, while integration of derivative we get function back. Integration also called derivative. Differentiation and Integration