Completing form is to solve a quadratic equation by changing the form of the equation so that the left side is a perfect square trinomial. Completing the square is a technique for converting a quadratic polynomial of the form ax2 + bx + c to a(x-b)2+c. Hence this method is used to convert. Similarly it use to […]
You are browsing archives for
Category: IB Maths SL
Integration of Polynomials
In integration the power of polynomials increase like quadratic become cubic etc. As well as get integration constant . It always give general solution due to integration constant. Integration
Function
A functions f(x) tells you what to do with the input, but, to be completely defined, function also need to know what type of input is permitted to go into the function. Function
Integration by substitution -1
This post is about worksheet of Integration by exponential substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by exponential substitution
Probability (Basic)
It is the measure of the likelihood that an event will occur. A number between zero and one that shows how likely a certain event. Another probability of event A is the number of ways event A can occur divided by the total number of possible outcomes. Also expressed by the ratio of the number of actual […]
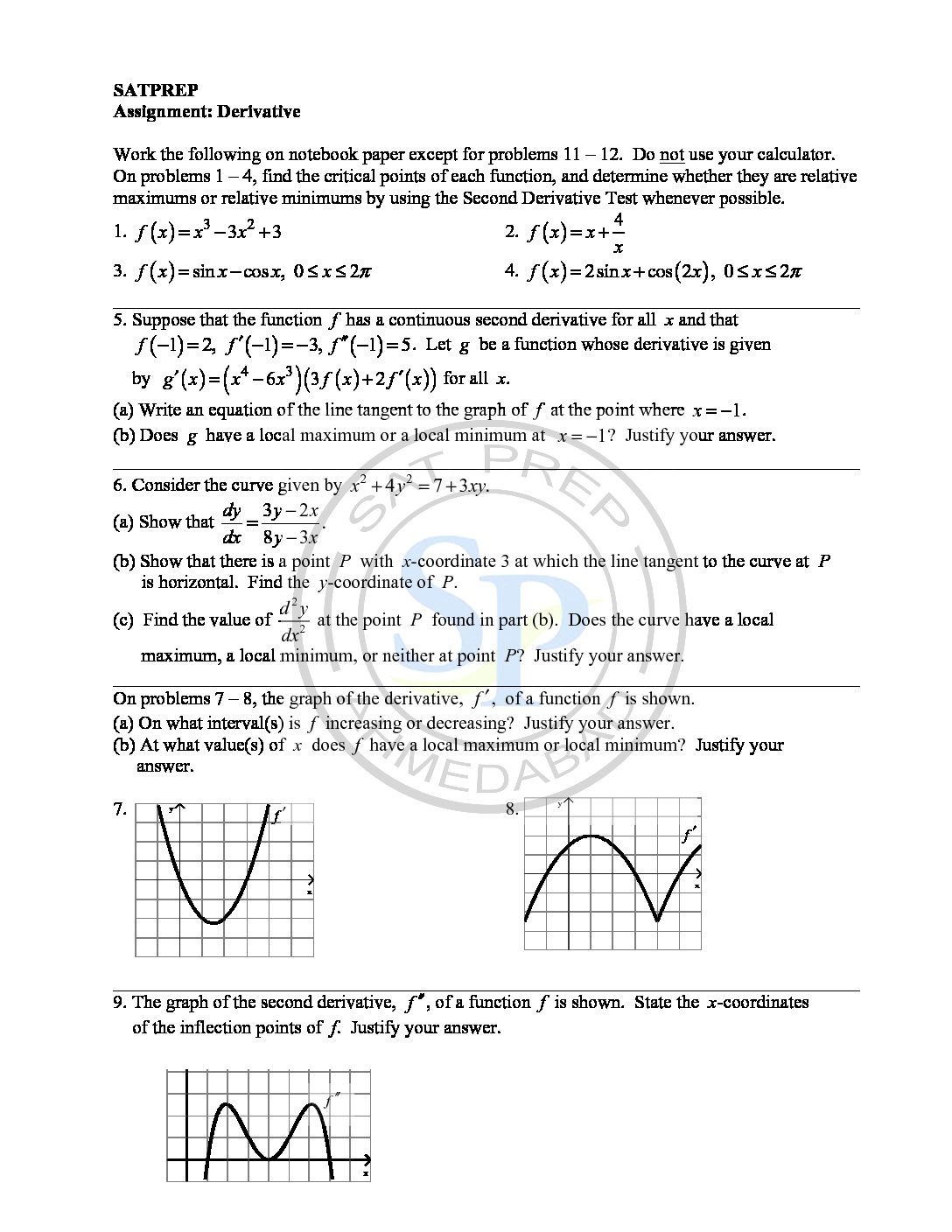
Derivative
The derivative of a function of a single variable at a chosen input value. Derivative is the slope of the tangent line to the graph of the function at that point. Hence derivative of a function y = f(x) of a variable x is a measure of the rate at which the value y of the function changes with respect to the change […]
Curve sketching
Curve Sketching. If f (-x) = -f (x) for all x in the domain, then f is odd and symmetric about the origin. d) Asymptotes: Find the asymptotes of the function using the methods described above. First attempt to find the vertical and horizontal asymptotes of the function. Curve sketching
Curve Sketching -2
the sketching of curve though coordinate of turning and axes intercepts . So equation of the curve is given. Curve sketching
Curve sketching
Coordinate of turning point and axes intercepts for the sketching of curves though . So equation of the curve is given. Curve sketching
Derivative of polynomials
Derivative is product of differentiation. Differentiation has applications to nearly all quantitative disciplines. For example, in physics, the derivative of the displacement of a moving body with respect to time is the velocity of the body, and the derivative of velocity with respect to time is acceleration. Therefore differentiation is process Derivative