In this post, First of all about derivatives and the various applications of derivatives. Derivative can be described as the slope at a point on a line around the curve and it is the most basic tool of calculus. It is also the rate of change at which one quantity changes with respect to another. How to find extrema using […]
You are browsing archives for
Category: mc
Derivative curve sketching
This post about tips to sketch derivative curve from curve . Therefore, we have to analyse curve like their intercepts , stationary point slope . derivative curve
Differentiation rule using table
In this post table containing values of differentiable functions f (x), g(x) and their derivatives. Use the table data and the rules of differentiation to solve each problem. Derivative Rules. The Derivative tells us the slope of a function at any point. Therefore rules we can follow to find many derivatives. Further more it is derivate of function. All above it is application of derivative Differentiation table rule
Sequences and Series
Sequences and series is arrangement of term in particular pattern. Mathematical structures using the convergence properties of sequences. In particular, sequences are the basic for series sequence and series
Equation of curve
Equations of curve evaluate by doing integration of derivative curve. The gradient and a point the curve passes through are given as.. Gradient: dy/dx = 6sqrt(x) Point the curve passes through: (4,1) I need to find the equation of the curve. Therefore integration is process of finding equation of the curve. Equation of curve
Binomial Theorem
When a binomial is raised to whole number powers, the coefficients of the terms in the expansion form a pattern. Each expansion has one more term than the power on the binomial. The sum of the exponents in each term in the expansion is the same as the power on the binomial. www.kutasoftware.com
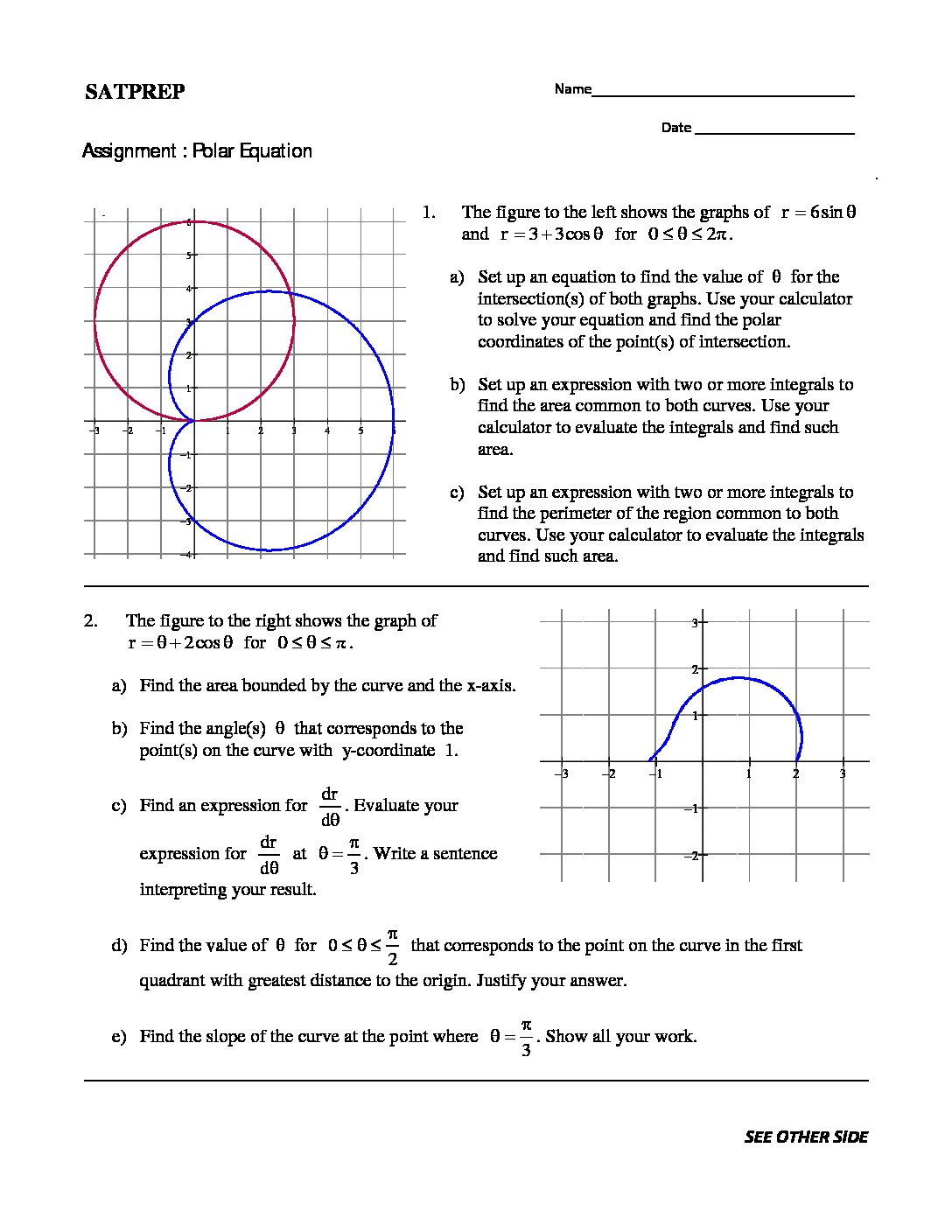
Derivative of polar equation
This post is about derivatives of Polar Equations. Because of polar equation, Polar equation like parametric equations of the curve where the angle θ is parameter. As well as equations have parameter (r,θ). For this polar equation, the parametric equations are x ( θ) = cos θ and y ( θ) = sin θ. Therefore, the derivative is which […]
Derivative of Polar Equation
This post is about derivatives of Polar Equations. Because of polar equation, Polar equation like parametric equations of the curve where the angle θ is parameter. As well as equations have parameter (r,θ). For this polar equation, the parametric equations are x ( θ) = cos θ and y ( θ) = sin θ. Therefore, the derivative is which […]
Area Under the Curve
This post about Area under a Curve. The area between the graph of y = f ( x ) and the x -axis is given by the definite integral. This formula gives a positive result for a graph above the x -axis, and a negative result for a graph below the x -axis. Because of enclosed region by limit. Hence , we use definite integration. Similarly for volume […]
Area between the curve
area between curves y = f (x) between x = a and x = b, integrate y = f (x) between the limits of a and b. Areas under the x-axis will come out negative and areas above the x-axis will be positive. Area