The expansion of two terms is know as Binomial theorems . Another way it is generalised form of expansion. Due to expansion of two term it is binomial. “What are the binomial coefficients?” . It shows how to calculate the coefficients in the expansion of (a + b) n. The symbol for a binomial coefficient nCr. As well as […]
You are browsing archives for
Category: Pure Maths
Imaginary No
A number is an imaginary number when it multiplied by square root of negative no. An imaginary number is the square root of a negative number and does not have a tangible value.”Complex” numbers have two parts, a “real” part (being any “real” number that you’re used to dealing with) and an “imaginary” part (being any number with an […]
Properties of indices
Laws of Exponents. Exponents are also called Powers or Indices. The exponent of a number says how many times to use the number in a multiplication. Law of Indices. To manipulate expressions, we can consider using the Law of Indices. These laws only apply to expressions with the same base, for example, 3 4 and 3 2 can be manipulated […]
Differentiation of polynomial
Differentiation is process of getting derivative. Differentiation has applications to nearly all quantitative disciplines. For example, in physics, the derivative of the displacement of a moving body with respect to time is the velocity of the body, and the derivative of velocity with respect to time is acceleration. Similarly in chemistry as well as Economics also derivative
Formulae of Calculus
List of Calculus Formulas-basic Properties and Formulas of Integration : If f (x) and g(x) are differentiable functions . Another In basic calculus, we learn rules and formulas for differentiation, which is the method by which we calculate the derivative of a function, and integration, Differential Calculus that is concerning rates of change and slopes of curves, and Integral Calculus concerning […]
Integration by Substitution-5
This post is about worksheet of integration by substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by substitution
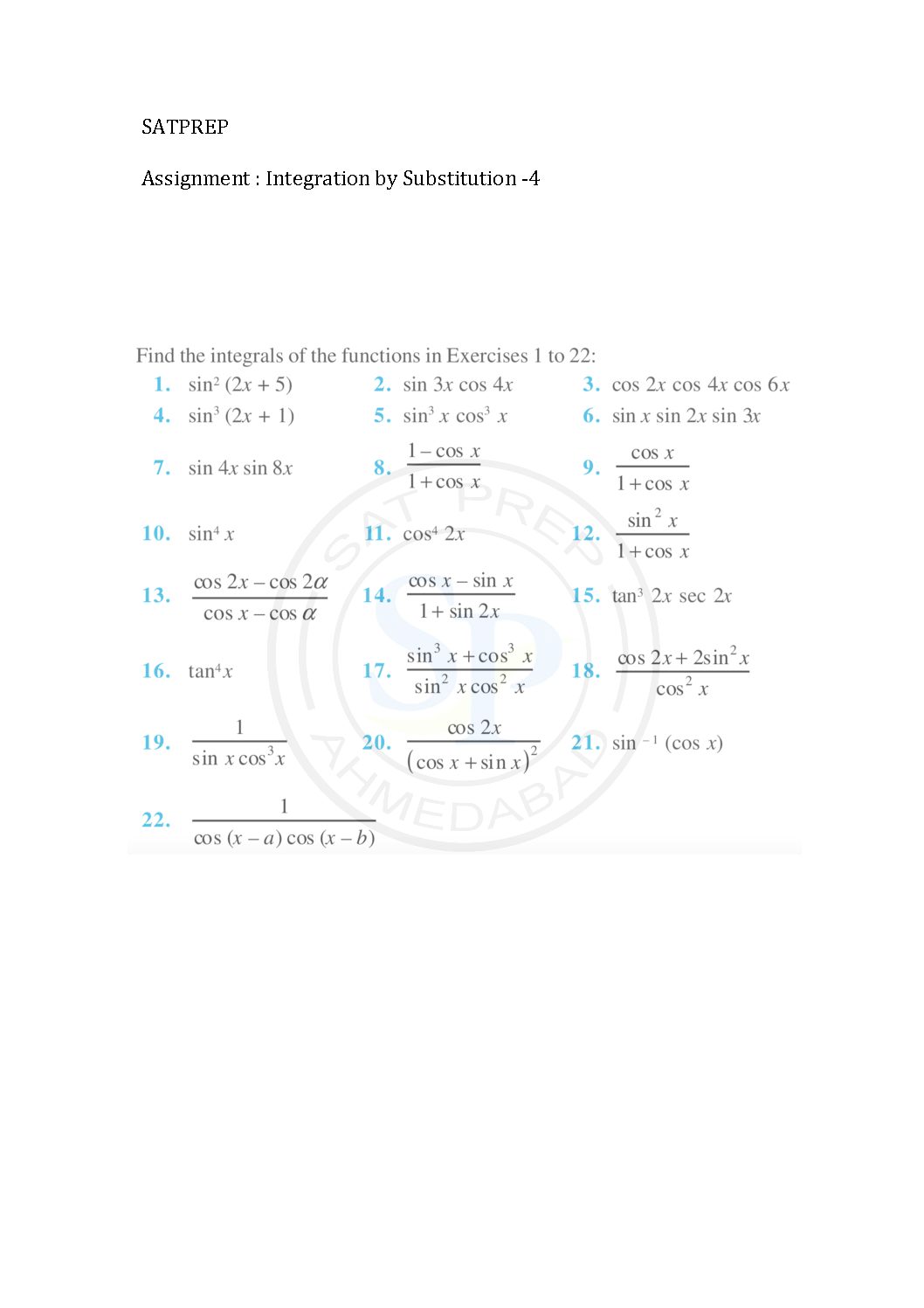
Integration by Substitution-4
This post is about worksheet of integration by substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] integration by substitution
integration by algebraic substitutions
This post is about worksheet of integration by algebraic substitutions. It also one of most important concept of integral calculus . The function ƒ(φ(t))φ′(t) is also integrable on [a,b] Integration by substitution
Integration of Radicals
This post about integration of polynomial with fractional power. First of all simplify expression also surds and then apply integration rule. Due to presence of constant it will give general solution. Integration
Trigonometric Identity
Trigonometric identities showing that the identity is always true, no matter what value of x or θ is used. Because it has to hold true for all values of x, we cannot simply substitute in a few values of x to “show” that they are equal. We have to use logical steps to show that one […]